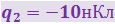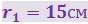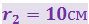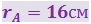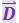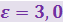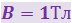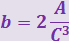К содержанию

Задача 3.1

В вершинах квадрата находятся равные отрицательные заряды q, а в центре – положительный заряд . Какой должна быть величина отрицательных зарядов, чтобы вся система находилась в состоянии равновесия?

Задача 3.2

Электрическое поле создано двумя точечными зарядами и . Расстояние между зарядами . Определить напряжённость электрического поля в точке, находящейся на расстоянии от первого и на расстоянии от второго зарядов.

Задача 3.3

Точечный заряд находится в центре сферы радиусом , равномерно заряженной с поверхностной плотностью заряда . Найдите силу, действующую на заряд , который последовательно помещают сначала в точку А, а затем в точку В. Точка  А находится на расстоянии от центра сферы, а точка В – на расстоянии . Изобразите графически E(r), где r – расстояние от центра сферы.

Задача 3.4

Тонкий стержень длиной (рис. 3.4.4) несёт равномерно распределённый по длине заряд с линейной плотностью . На расстоянии от стержня находится заряд . Заряд равноудалён от концов стержня. Определить силу взаимодействия точечного заряда с заряженным стержнем.

Задача 3.5

Отрезок длиной , равномерно заряженный с линейной плотностью , и бесконечная прямая нить, заряженная с линейной плотностью , расположены в одной плоскости перпендикулярно друг другу на расстоянии (рис. 3.5.5). Определить силу взаимодействия между ними.

Задача 3.6

Найти работу, которую нужно затратить, чтобы вынуть диэлектрик, расположенный между обкладками плоского конденсатора, для двух случаев: когда заряд на обкладках является постоянным и равным q и когда напряжение между обкладками поддерживается постоянным и равным U. Площадь пластин конденсатора и расстояние между пластинами равны соответственно S и d. Толщина диэлектрика равна , а его диэлектрическая проницаемость ε.

Задача 3.7

Электростатическое поле в вакууме создаётся системой одинаковых по модулю точечных зарядов . Найдите потоки векторов и через произвольную замкнутую поверхность S (рис. 3.7.7). Как изменятся эти потоки, если систему поместить в среду с диэлектрической проницаемостью ?

Задача 3.8

Конденсатор ёмкостью был заряжен до разности потенциалов 40 B. После отключения от источника тока конденсатор был соединён параллельно с другим незаряженным конденсатором ёмкостью . Какое количество энергии первого конденсатора израсходуется на образование искры в момент присоединения второго конденсатора?

Задача 3.9

Электрон, ускоренный разностью потенциалов U = 6 кВ, влетает в однородное магнитное поле под углом α = 30° к направлению поля и начинает двигаться по винтовой линии. Индукция магнитного поля . Найти радиус витка винтовой линии.

Задача 3.10

Заряд q влетает с постоянной скоростью в однородное магнитное поле перпендикулярно линиям индукции. Индукция магнитного поля . В течение параллельно индукции магнитного поля действует электрическое поле напряжённостью . Вычислить постоянный шаг спиральной траектории заряда.

Задача 3.11

В однородном магнитном поле, индукция которого 0,1 Тл, движется проводник длиной 10 см. Скорость движения проводника 15 м/с направлена перпендикулярно магнитному полю. Чему равна индуцированная в проводнике э.д.с.?

Задача 3.12

Тонкий, равномерно заряженный диск, вращается вокруг своей оси с угловой скоростью ω (рис. 3.12.12а). Определить индукцию магнитного поля в центре диска, если радиус диска R, а поверхностная плотность заряда ω.

Задача 3.13

По сплошному цилиндрическому проводнику радиусом R течёт ток плотности j (рис. 3.13.13). Определить индукцию магнитного поля внутри и вне проводника.

Задача 3.14

В плоскости квадратной рамки с омическим сопротивлением R = 7 Ом и стороной a = 20 см расположен на расстоянии r0 = 20 см от рамки бесконечный проводник (рис. 3.14.14). Сила тока в проводнике изменяется по закону I = b ⋅ t3, где . Проводник параллелен одной из сторон рамки. Определить силу тока в рамке в момент времени t = 10 с.

Задача 3.15

Длинный прямой проводник с током I и П-образный проводник с подвижной перемычкой расположены в одной плоскости (рис. 3.15.15). Перемычку, длина которой , перемещают с постоянной скоростью v. Найти э.д.с. индукции в контуре как функцию расстояния r.

Задача 3.16

Длинный цилиндрический конденсатор заряжается от источника э.д.с. Доказать, что ток смещения в диэлектрике, заполняющем пространство между обкладками конденсатора, равен току в цепи источника э.д.с. Искажениями поля у концов конденсатора пренебречь.