ФИЗИКА

Задача 3.12. Тонкий, равномерно заряженный диск, вращается вокруг своей оси с угловой скоростью ω (рис. 3.12.12а). Определить индукцию магнитного поля в центре диска, если радиус диска R, а поверхностная плотность заряда ω.

Рис. 3.12.12

Задачу можно решить двумя способами.

1. Заменим заряженный вращающийся диск моделью поверхностно распределённого тока. Эту модель, разделив диск на столь узкие кольцевые зоны, чтобы каждую из них можно было принять за тонкий кольцевой проводник, представим совокупностью моделей линейного кругового тока. Ток такого кольца создаёт (3.5.29) в точке О  индукцию

(3.12.1)

.

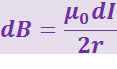Выбрав в качестве переменной интегрирования величину dr, выразим dI через dr и параметры, заданные в условии задачи. По определению 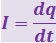. Применительно к нашему случаю, эта формула запишется так

(3.12.2)

,

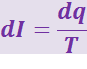где

(3.12.3)

.

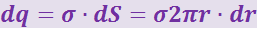
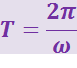Подставляя (3.12.3) в (3.12.2), получим:

(3.12.4)

.

Подставив (3.12.4) в (3.12.1), будем иметь:

.

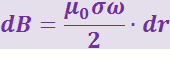Интегрируя, получим:

(3.12.5)

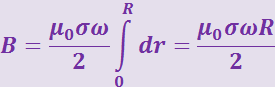
2. Заменим заряженный вращающийся диск моделью движущегося поверхностно распределённого заряда. Эту модель, разделив диск на элементы dS, несущие заряд dq, представим совокупностью моделей точечных зарядов. Деление на элементы dS выполним следующим образом: сначала разделим диск на кольцевые зоны шириной dr, а затем радиальными прямыми, исходящими из точки О, разделим на элементы dS. Радиальные прямые проведём таким образом, чтобы угол между двумя соседними прямыми был равен dφ.

Поскольку площадь dS мала будем считать её прямоугольником. Тогда (рис. 3.12.12в):

(3.12.6)

,

где r – расстояние от элемента до точки О.

Заряд dq этого элемента создаёт в точке О индукцию:

(3.12.7)

,

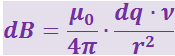где

(8)

;

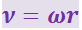ν - линейная скорость заряда dq.

Выберем в качестве переменных интегрирования величины dr и dφ и выразим dq через параметры, заданные в условии задачи, и переменные интегрирования

.

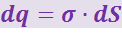Подставив в эту формулу (3.12.6), будем иметь:

(3.12.9)

.

Наконец, подставив (3.12.9) и (3.12.8) в (3.12.7), получим:

(3.12.10)

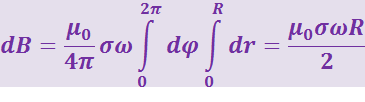
После интегрирования будем иметь:

(3.12.11)

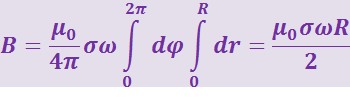
Сравнивая (3.12.5) и (3.12.11) видим, что результат, естественно, одинаков.

к к к