ФИЗИКА

3.8. УРАВНЕНИЯ МАКСВЕЛЛА

Ранее нами были рассмотрены основные законы электрических и электромагнитных явлений: теорема Гаусса, закон полного тока и закон электромагнитной индукции. Эти законы, являющиеся обобщением экспериментальных фактов, позволяют решать основную задачу, возникающую при изучении электромагнитных явлений: по заданному распределению зарядов и токов отыскать созданные ими в каждой точке пространства электрические и магнитные поля.

Максвелл обобщил эти законы и разработал законченную теорию единого электромагнитного поля, создаваемого произвольной системой зарядов и токов.

Теория Максвелла представляет собой феномелогическую теорию электромагнитного поля. Это означает, что внутренний механизм явлений, происходящих в среде и вызывающих появление электрических и магнитных полей, в теории не рассматривается.

Электрические и магнитные свойства среды характеризуются в теории Максвелла тремя величинами: относительной диэлектрической проницаемостью ε, относительной магнитной проницаемостью μ и удельной электропроводностью γ. Зависимость этих величин от свойств среды, физический смысл тех явлений, которые происходят в ней при поляризации и намагничивании в теории Максвелла не исследуются.

Теория Максвелла является макроскопической теорией электромагнитного поля. В ней рассматриваются электрические и магнитные поля, создаваемые макроскопическими зарядами и токами, т.е. зарядами, которые сосредоточены в объёмах, неизмеримо больших, чем объёмы отдельных атомов и молекул. Кроме того предполагается, что расстояния от источников полей до рассматриваемых точек пространства также во много раз больше размеров молекул. Поэтому заметные изменения полей, исследуемых в теории Максвелла, возможны только на протяжении расстояний, огромных по сравнению с размерами атомов и молекул. Наконец, периоды изменения переменных электрических и магнитных полей должны быть во много раз больше периодов внутримолекулярных процессов.

В действительности, макроскопические заряды и токи представляют совокупности макроскопических зарядов и токов, которые создают свои электрические и магнитные поля, непрерывно изменяющиеся в каждой точке пространства. Поэтому и результирующие электрическое и магнитное поля всегда являются переменными. Эти поля получили название микрополей.

Из сказанного следует, что в теории Максвелла рассматриваются усреднённые электрическое и магнитное поля, причём усреднение соответствующих микрополей производится для интервалов времени значительно больших периодов обращения или колебания элементарных зарядов и для участков поля, объёмы которых во много раз больше объёмов атомов и молекул.

Теория Максвелла основана на том, что электрические и магнитные взаимодействия происходят при посредстве электрических и магнитных полей, в которых они распространяются со скоростью света в данной среде.

Математическим выражением теории Максвелла служат четыре уравнения Максвелла, которые принято записывать в двух формах: интегральной и дифференциальной. Уравнения Максвелла в интегральной форме выражают соотношения, справедливые для мысленно проведённых в электрическом поле неподвижных замкнутых контуров и поверхностей. Уравнения Максвелла в дифференциальной форме показывают, как связаны между собой характеристики электромагнитного поля и плотности электрических зарядов и токов в каждой точке этого поля. Здесь мы ограничимся рассмотрением только интегральной формы уравнений Максвелла.

Дифференциальные уравнения Максвелла получаются из интегральных с помощью двух теорем векторного анализа: теоремы Гаусса и теоремы Стокса.

Теорема Гаусса утверждает: поток вектора , характеризующего какое-либо поле, через произвольную замкнутую поверхность S, мысленно проведённую в этом поле, равен интегралу от дивергенции вектора , взятого по объёму V, ограниченному замкнутой поверхностью S

(3.8.1)

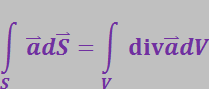
Теорема Стокса утверждает: циркуляция вектора , характеризующего какое-либо поле, вдоль произвольного замкнутого контура, мысленно проведённого в этом поле, равна потоку вектора через поверхность S, натянутую на контур

(3.8.2)

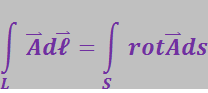
С понятием дивергенции мы познакомились в п. 3.1.6. Очень кратко познакомимся с понятием ротор.

Ротор соотносится с циркуляцией подобно тому, как дивергенция соотносится с потоком: дивергенция порождает поток, ротор порождает циркуляцию.

Циркуляция обладает свойством аудитивности. Это означает, что циркуляция по контуру, ограничивающему несколько смежных поверхностей, равна сумме циркуляций по контурам, ограничивающим каждую из поверхностей в отдельности.

Из свойств аудитивности вытекает, что элементарная циркуляция пропорциональна не длине контура, а поверхности элементарной площадки, охватываемой контуром. Это даёт основание утверждать, что циркуляция порождается на поверхности. Соответственно можно ввести понятие плотности порождения циркуляции, т.е. циркуляции, порождаемой бесконечно малым участком поверхности в расчёте на единицу площади этого участка:

плотность порождения циркуляции

(3.8.3)

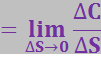
где – элементарная циркуляция.

Величина (3.8.3), вычисленная для некоторой точки поля Р, будет зависеть не только от свойств поля в этой точке, но также и от ориентации в пространстве площадки , т.е. ориентации контура, охватывающего . Эта ориентация может быть задана направлением положительной нормали к плоскости контура (положительной считается нормаль, связанная с направлением обхода контура при вычислении циркуляции правилом правого винта). Определяя предел (3.8.3) в одной и той же точке Р для разных направлений мы будем получать различные значения.

Таким образом, плотность порождения циркуляции ведёт себя при вращении контура как проекция вектора на нормаль к контуру. Этот вектор называют ротором векторного поля и обозначают .

к к к