ФИЗИКА

3.8.3. Третье и четвёртое уравнения Максвелла

Максвелл обобщил теорему Гаусса для электростатического поля (3.2.19). Он предположил, что она справедлива для любого электрического поля, как стационарного, так и переменного. Соответственно третье уравнение Максвелла в интегральной форме имеет вид:

(3.8.20)

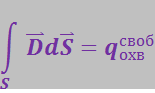
или

(3.8.21)

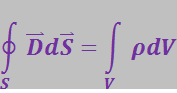
Здесь ρ – объёмная плотность свободных зарядов, а интегрирование в правой части уравнения (3.8.21) проводится по объёму V, ограниченному замкнутой поверхностью S.

Максвелл предположил также, что всякое магнитное поле (в вакууме или в среде, стационарное или переменное) всегда соленоидально. Иными словами он обобщил теорему Гаусса (3.5.41) на любое магнитное поле.

Соответственно четвёртое уравнение Максвелла в интегральной форме имеет вид:

(3.8.22)

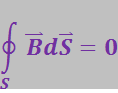
С помощью теоремы Гаусса (3.8.1) можно перейти от интегральных уравнений Максвелла (3.8.21) и (3.8.22) к дифференциальным. Третье уравнение Максвелла в дифференциальной форме выглядит следующим образом:

(3.8.23)

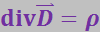
Четвёртое уравнение Максвелла в дифференциальной форме имеет вид:

(3.8.24)

к к к