в Содержание

Перечень тем

Тема 15

ТОЧНОСТЬ МЕТОДА АНАЛИЗА

Точность метода анализа - его характе­ристика, в которой необходимо различать две стороны: воспроизводимость и правильность.

Воспроизводимость измеряют от­клонением отдельных результатов от среднего значения, правильность - отклонением среднего значения содержания от истинного.

Воспроизводимость устанавливается по обычным правилам статистической обработки результатов. Проводят параллельные (контрольные) определения 5% образцов, т.е. берут каждый двадцатый анализируемый образец. На­пример, при определении фосфора на фотоэлектронном колори­метре допустимы расхождения результатов между повторностями анализа до 10% (0,01 мг / 100 г почвы). Если рас­хождения между результатами анализа превышают до­пустимые, анализ повторяют.

Математическая теория погрешностей требует определения еще одной величины - точности прямого измерения (е). Эту величину определяют по уравнению, вывод которого можно най­ти в математической теории погрешностей. При использовании этого уравнения задаются значения надежности (а), т.е. до­лей случаев, в которых при данном числе измерений среднее арифметическое лежит в определенных пределах. При физико-химических и аналитических измерениях принимают а = 0,95 или 0,99.

Это означает, что 95 или 99% всех из­мерений лежит в указанных пределах.

Предельное разбавление показывает, при каком разбавлении данный элемент еще может быть обнаружен, и выражается от­ношением массы обнаруживаемого элемента к общей массе рас­творителя. Например, предельное разбавление 1:40000 означа­ет, что метод позволяет обнаруживать одну часть элемента в 40000 частях раствора.

Чувствительность также характеризуют минимально обнару­живаемой концентрацией, т.е. наименьшей концентрацией дан­ного вещества, обнаруживаемого в данных условиях данным методом в единицах массы на единицу объема (моль/л или мкг/мл). В ряде случаев чувствительность выражают в процен­тах. Предел чувствительности зависит от способа выполнения реакции и других факторов.

При инструментальных методах анализа показания любого прибора служат мерой количества определяемого элемента; для оценки предела чувствительности, т.е. величины разности полезного сигнала и сигнала контрольного опыта или фона прибора, применяют статистические методы. Минимально определяемое содержание элемента с допустимым уровнем надежности, выра­жаемое в массовых единицах, - это абсолютный предел чувствительности. Минимально определяемое количество элемента, выражаемое в процентах или частях на миллион, - это относи­тельный предел чувствительности. Для увеличения чувствитель­ности метода необходимо увеличить отношение полезного сигна­ла к фону.

Для сравнения возможностей различных методов иногда чувствительность выражают в граммах в пробе или просто в грам­мах. В таком случае количествоо пределяемого элемента или соединения относят к минимальной пробе, необходимой для ана­лиза этим методом. Сравнительную чувствительность в этом случае можно представить как отрицательный логарифм вели­чины чувствительности в граммах. Например, если чувствитель­ность составляет 10–10 г, то -lg10–10 = 10. Для того чтобы как-то сопоставить количество примеси в единицах массы с молекуляр­ной шкалой концентрации, обычно берут среднюю молекуляр­ную массу условного вещества, равную 100, учитывая, что атом­ная и молекулярная массы большинства простых веществ нахо­дятся в пределах от 10 до 250.

Границу чувствительности некоторых методов можно про­иллюстрировать следующими примерами: весовой и объемный анализы - 10-2...100%, колориметрия - 10-5...100%, кулонометрия - 10-3...100%, нефелометрия - 10-8...10-4  …  100 %, полярография - 10–4... 10-1 …100 %.

Поскольку обычно анализируют большое количество проб, несколько различающихся по составу, значительную роль игра­ет, с одной стороны, воспроизводимость, т.е. близость полученных результатов к какой-то средней величине, а с другой сто­роны - избирательность (селективность), т.е. возможность оп­ределения какого-то элемента в присутствии других.

В зависимости от чувствительности и количества материала, которое с их помощью можно установить, методы физико-хими­ческих анализов малых концентраций можно квалифицировать как макро- (более 10–1г), полумикро- (10–2...10–1г), микро- (10–3...10–2г), ультрамикро- (10–7...10–4г) и субмикрометоды (10–9...10–7 г).

Погрешности можно выразить в абсолютных единицах с раз­мерностью определяемых величин (мг, моль, моль/л и т. д.) и относительных (обычно %).

При обсуждении пригодности и вариантов применения разных аналитических методов для определения концентрации загрязнителей прежде всего обращается внимание на чувствительность и предел обнаружения этих методов. Чувствительность (Н) метода можно рассчитать по данным калибровки измерительного прибора (фотоколориметра, спектрофотометра и т.д.). При калибровке, используя растворы с известным содержанием загрязнителя, экспериментально строят зависимость некоторого фиксируемого физического параметра (оптической плотности, силы тока и т.п.) от концентрации или количества загрязнителя в пробе. На графике концентрация откладывается по оси  абсцисс (х), а физический параметр - по оси ординат (у). Тогда

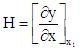
или

где D - оптическая плотность;

С - концентрация, так как в аналитической химии, как правило, используется линейная часть градуировочного графика.

Предел обнаружения метода (наименьшая концентрация Сm, которая может быть обнаружена с разумной достоверностью) можно рассчитать по формуле

где σф - средняя квадратическая погрешность отдельного измерения фона уф, найденная по формуле

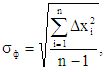
и результатам экспериментального определения фона или через минимально определяемое значение физического параметра по калибровочному графику:

-уm = -yф + 3σф

Если предел обнаружения загрязнителя выше, чем его ожидаемая концентрация в объекте окружающей среды, необходимо провести концентрирование загрязнителя.

Для этой цели наиболее часто используется экстракция, реже - хроматография. Необходимый коэффициент концентрирования получают из сопоставления предела обнаружения метода и ожидаемой концентрации загрязнителя.

Статистическая обработка данных лабораторных анализов. При статистической обработке данных анализов ошибки подразделяют на систематические и случайные. Систематические ошибки вызываются факторами, действующими одинаковым образом при многократном повторении анализа. При­мером такой ошибки может служить взвешивание на весах с по­мощью гири. Если гиря имеет ошибку в 0,1 г, то результат взве­шивания будет всегда заниженным или завышенным на эту вели­чину.

Источниками систематических ошибок могут быть: неисправности измерительной аппаратуры; индивидуальные особенности экспериментатора (субъективные); ошибки, обусловленные методом анализа.

Случайные ошибки связываются с такими факторами, как колебание чашек весов, изменения в соответствии органов чувств, участвую­щих в измерении, колебания в освещенности рабочего места и т.д.

Ошибку измере­ния, вызванную этими факторами, можно рассматривать как случайную. Влияние случайных ошибок на результат анализа можно количественно оценить при помощи математической статистики. Случайную ошибку называ­ют также статистической. Она зависит от количества определений. Следовательно, при увеличении повторностей анализа, при увеличении количества параллельных образцов случайная ошибка может составлять малую величину.

Подразделение ошибок на систематические и случайные услов­но для конкретных условий каждого измерения.

Если источник систематической ошибки извес­тен и устранить его невозможно, то влияние фактора, вызываю­щего эту ошибку, на результат измерений можно оценить стати­стически.

К систематическим ошибкам относятся погрешности измери­тельных приборов, которые определяются классом точности при­бора. Если на приборе указан класс точности 1, то это означает, что показания прибора правильны с точностью до 1% от всей действующей шкалы прибора. Иначе говоря, прибор, шкала кото­рого имеет 100 делений, дает ошибку в измерении не более 1 де­ления. Очевидно, что нет никакого смысла брать отсчеты менее одного де­ления. Приборы характеризуются классом точности в пределах от 0,05 до 4. Более грубые приборы обозначения класса не имеют.

Каждый измерительный прибор, вне зависимости от класса точности, обладает определенным интервалом чувствительности, т.е. наименьшим значением измеряемой величины, которое при­бор в состоянии различить. Этот интервал чувствительности ограничивает разрешающую способность прибора.

Результаты анализа выражаются количественными данными. Повторные анализы или анализы параллельных образцов дают ряд величин, представляющих собой выборку.

В задачу стати­стической обработки анализов входит:

1) определение основных параметров выборки (средняя арифметическая-х, дисперсия S2, среднее квадратическое отклонение S, коэффициент вариации V, ошибка сред­ней S-х ); 

2) соотнесение выборочных параметров с параметрами генеральной совокупности или с некоторой конкретной измеряе­мой величиной.

По полученной выборке проводят вычисления:

- средней арифметической, дисперсии, среднеквадратического отклонения;

- коэффициента вариации, или ошибки параллельных определений.

Коэффициент вариации, или ошибка параллельных определений (%), рассчитывается по формуле

Cv = σ   100 /-х.

Если изменчивость по параллельным определени­ям незначительна, то испытанный метод определения дает хорошую воспроизводимость.

Считается, что если Cv:

- не превышает 10% - изменчивость незначительна;

- выше 10% - средняя;

- более 20% - значи­тельная.

Точность определений, рассчитанную по разнице и ошибке разницы сред­ней, т.е. по критерию Стьюдента, оценивают из соотношения полученного t фактического и t теоретического, или табличного. Если tпракт < t теор, то средние арифметические различаются незначительно.

Оба метода в пределах ошибок опыта дают одинаковые результаты, или сравниваемые результаты однозначны.