Тема 14

14.2.2. Наиболее распространенные способы статистической обработки

14.2.2.1. Метод попарного сравнения вариантов путем нахождения границ их вариации

На практике наиболее простым способом статистической обработки является, как и в первом случае, определение величины среднего квадратического отклонения с учетом числа степеней свободы

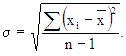
где n - объем выборки, т.е. число повторностей в варианте;

n - 1 - число степеней свободы (обозначается также буквами df);

хi - значение каждой повторности;

-х - среднее арифметическое варианта;

Σ(хi - -х )2 - сумма квадратов отклонений.

Среднее квадратическое отклонение позволяет установить пределы вариаций средних арифметических двух сравниваемых групп (вариантов).

Пример. Допустим, изучают действие различных доз нитратов аммония на образование хлорофилла в листьях растений. Результаты повторностей и средние по вариантам записывают в табл. 15.

Таблица 15

Влияние дозы нитрата аммония на содержание хлорофилла в листьях растений, мг/дм2

Затем для каждого из сравниваемых вариантов составляют вспомогательную таблицу, где помещают результаты каждой повторности и рассчитывают среднюю арифметическую по формуле

-х = Σхi  / n.

Определив,-х, вычисляют и вносят в табл. 16. отклонения от средней (хi --х) и среднее квадратическое отклонение (хi  --х )2

Таблица 16

Содержание хлорофилла в растениях, мг/дм2

Подставляя числовые значения в формулу среднего квадратического отклонения

находят 

т.е. среднее квадратическое отклонение для варианта 1 равно ± 0,1.

Обычно его помещают в окончательной табл. 17 справа от средней арифметической  варианта.  Например, для первого варианта: 4,0± 0,1.

Таблица 17

Достоверность изменения содержания хлорофилла в растениях, мг/дм2

Подобным образом определяют среднее квадратическое отклонение и для других вариантов опыта и заносят в табл. 17.

В опыте среднее квадратическое отклонение для варианта ΙΙ оказалось равным 3,7 ± 0,17, а для варианта ΙΙΙ - 3,5 ± 0,26.

Устанавливают, достоверна ли разница между вариантом с внесением полной дозы и вариантом с внесением половинной дозы аммиачной селитры. Среднее квадратическое отклонение показывает, что значения средней арифметической для варианта Ι колеблются в пределах 4,1-3,9, а для варианта ΙΙ - 3,87-3,53.

Значения нижнего предела для варианта Ι - 3,9 и верхний для варианта ΙΙ - 3,87 близки к перекрыванию, т.е. достоверность слабая, но существует тенденция к достоверной разнице между вариантами. Если значения нижнего предела одного варианта и верхний предел другого варианта перекрываются, то достоверность отсутствует.

Значения вариации средних для варианта Ι и контроля, составляющие 4,1-3,9 и 3,76-3,24, не перекрывают друг друга, следовательно, разница между ними достоверна.

Результаты расчетов можно выразить графически, отложив на оси ординат средние арифметические вариантов и размах их вариаций. Обычно, чем больше объем выборки, т.е. n, тем выше точность определения средней арифметической и меньше размах ее колебаний. При n > 30 с учетом ошибки (5%) средние арифметические выборочных совокупностей (вариантов) будут находиться в пределах х ± 2,58σ. В этом случае достоверность разницы между вариантами можно определить, не прибегая к приведенным выше расчетам. Если эта разница превышает произведение σ, установленное для каждого варианта, на 2,58, то она достоверна.

14.2.2.2. Оценка существенности разности выборочных средних по t-критерию

При сравнении средних необходимо иметь в виду два случая:

1) сравниваются средние двух независимых выборок, когда единицы наблюдения первой выборки не связаны никаким общим условием с единицами наблюдения второй выборки;

2) сравниваются две сопряженные выборки, в которых единицы наблюдения первой выборки связаны (сопряжены) каким-то общим условием с единицами наблюдения второй выборки.

В первом случае по t-критерию Стьюдента оценивается существенность разности средних (-d=-x1--x2), а во втором существенность средней разности (-d = Σ d / n ).

Достоверность разницы между средними арифметическими двух выборочных совокупностей можно установить, пользуясь значением средней квадратической ошибки S-х, которую рассчитывают по формуле

.

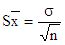Рассчитав среднюю квадратическую ошибку для одной S-х1 и другой S-х2 сравниваемых групп, определяют среднюю ошибку разницы Sd по формуле:

находят разницу между средними арифметическими этих двух групп:

d =-х1 --х2.

Значения величины средней квадратической ошибки для каждой группы, средних ошибок разницы Sd и разницы между средними арифметическими d помещают в табл. 18.

Таблица 18

Достоверность изменения содержания хлорофилла в растениях, мг/дм2

Критерий существенности разности. Гарантией надежности вывода о существенности или несущественности различий между-х1 и-х2 служит отношение разности между вариантами к ошибке этой разницы. Это отношение получило название критерия существенности разности:

Расчет. В опыте содержание хлорофилла в варианте Ι равно хсред ± σ = 4,0 ± 0,10, в варианте ΙΙ - 3,7 ± 0,17.

Значение средней квадратической ошибки для каждого варианта равно:

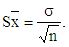
т.е. для вариантов

Значение средней квадратической ошибки по каждому варианту заносят в табл. 18. Затем по формуле

определяют среднюю ошибку разницы между вторым и первым вариантом:

По этой же формуле  определяют среднюю ошибку разницы между третьим и первым вариантом, изменив параметры второго варианта на параметры третьего:

Sd = 

 т.е. 

Значение средней ошибки разницы между вариантами заносят в табл.18.

Последовательно можно установить разницу между вторым и третьим вариантами, т.е. сделать попарное сравнение любых двух вариантов в опыте.

Далее устанавливают значение разницы между средними арифметическими вариантов Ι и ΙΙ: (d = 4,0-3,7 = 0,3), разницу заносят в табл.18.

Нормированное отклонение, или критерий существенности разности. Определив ошибку разницы Sd и разницу между средними арифметическими двух сравниваемых групп d, находят величину t, называемую нормированным отклонением:

Величину t, называемую нормированным отклонением, между вторым и первым вариантом расчитывают, разделив 0,3 на 0,116, и получают 2,59.

Величину t, между третьим и первым вариантом рассчитывают, разделив 0,5 на 0,16, и получают 3,13. Величины критерия t помещают в табл. 19.

Таблица 19

Достоверность изменения содержания хлорофилла в растениях (мг/дм2) с учетом величины коэффициента нормированного отклонения (критерия Стьюдента)

Достоверность разницы между двумя вариантами определяют сравнивая фактическое значение t с найденным по табл. 20.

Таблица 20

Коэффициенты нормированных отклонений

Для нахождения (tтабл) надо знать число степеней свободы df и принять необходимый уровень значимости (обычно при ошибке 5% он равен 0,95).

Число степеней свободы df может быть равным n - 1 или n1 + n2 - 2, т.е учитываются параметры либо внутри группы, либо между группами.

Если окажется, что tфакт<tтабл, то разница между средними недостоверна, если же tфакт>tтабл, то разница между средними достоверна. В нашем опыте число степеней свободы для расчета равно n1 + n2 - 2. Значит при уровне значимости 0,05 и df=(3+3)-2=4 tтабл равно 2,78.

Разница между средними в варианте с полной и в варианте с половинной дозой недостоверна.

Разница между средними в варианте с полной дозой селитры и в контрольном варианте по  величине коэффициента нормированного отклонения (критерия Стьюдента) достоверна.

14.2.2.3. Оценка существенности разности средних по наименьшей существенной разности

НСР05 и НСР01 - наименьшие существенные разности двух сравниваемых величин для 5%-го и 1%-го  уровня значимости, - величины, указывающие границы возможных случайных отклонений.

НСР рассчитывается при определенном уровне значимости по формуле:

НСР05 = t05 Sd,

НСР01 = t01 Sd.

Для представленного опыта для разницы между первым и вторым вариантом величина

НСР05 = t05 Sd = 2,78 • 0,116 = 0,32,

НСР01 = t01 Sd = 4,6 • 0,116 = 0,53.

Разница между средними вариантов должна быть больше НСР.

Разница между первым и вторым вариантом опыта составляет 0,3, а наименьшая существенная разница при разных уровнях достоверности выше. Значит, разница между полной и половинной дозой селитры в опыте незначительна.

Для разницы между первым и третьим вариантом величина

НСР05 = t05 Sd = 2,78 • 0,16 = 0,45,

НСР01 = t01 Sd = 4,6 • 0,16 = 0,73.

Разница между первым и третьим вариантом опыта составляет 0,5, а наименьшая существенная разница при разных уровнях достоверности 0,45 и 0,73. Значит, разница между полной дозой селитры и контролем в опыте достоверна при 5%-м уровне значимости и несущественна при 1%-м уровне значимости.