14.2. Примеры и алгоритм математической обработки
14.2.1. Наиболее краткая математическая обработка
Если х1, х2, х3…….,хn отдельные измерения искомой концентрации примеси (результаты параллельных определений), то находят среднее арифметическое по формуле
![]()
где n - число измерений, и вычисляют абсолютную случайную погрешность i-го измерения:
Δ х i = х i –-х.
Выделяют среднюю квадратическую погрешность отдельного измерения вычисляют
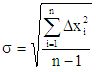 ,
,
затем относительную квадратическую погрешность отдельного измерения
![]()
Рассчитывают среднюю квадратическую погрешность (или отклонение) среднего арифметического:
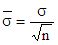 .
.
Затем рассчитывают относительную квадратическую погрешность среднего арифметического:
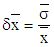 .
.
Истинное значение искомой концентрации примеси с надежностью (вероятностью) Р лежит в доверительном интервале
-х ± tp-σ,
где tp - коэффициент Стьюдента, зависящий от числа измерений и ожидаемой (заданной) надежности Р.
Если для некоторого i-го измерения |Δхi| > 3σ, то это измерение убирают как содержащее ошибку и все величины пересчитывают заново.