14.1.2. Характеристика воспроизводимости результатов анализа
Случайные ошибки предвидеть и учесть невозможно. Чтобы исключить влияние случайных ошибок на результат, определения в опыте проводят в нескольких повторностях. С увеличением числа повторностей повышается точность среднего арифметического до известного предела. Таким образом, уменьшается величина отклонения от действительного результата определения. Отклонение результатов отдельных определений от среднего арифметического характеризует воспроизводимость того или иного метода.
Абсолютная ошибка представляет собой разность между найденным результатом и истинным результатом определения.
Относительная ошибка представляет собой отношение абсолютной ошибки к измеряемой величине. Это отношение умножают на 100, чтобы выразить ошибку в процентах:
∆Хотн = (∆Х/mист) 100.
Об отсутствии случайных ошибок судят по воспроизводимости определений. Воспроизводимость устанавливают путем математической обработки результатов анализа, основанной на теории вероятности.
-Х = (х1 + х2 + ……. + хn) / n.
Если систематические ошибки отсутствуют и число измерений n велико (т.е. стремится к бесконечности), наблюдается нормальное (по закону Гаусса) распределение случайных ошибок (рис. 67); по оси абсцисс откладывают значения определяемой величины (х), а по оси ординат - вероятности получения их при анализе. Из рисунка видно, что:
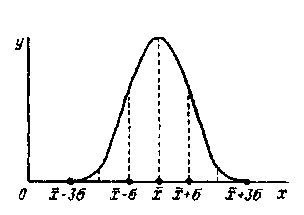
Рис. 67. Нормальное (по закону Гаусса ) распределение случайных ошибок
а) наиболее вероятным значением определяемой величины надо считать среднее арифметическое-Х из n определений хi;
б) одинаково вероятны отклонения от среднего арифметического как со знаком плюс, так и со знаком минус;
в) более вероятны малые отклонения от среднего арифметического, чем большие.
Поскольку как положительная ошибка, так и отрицательная характеризует отклонение от среднего арифметического, при вычислении воспроизводимости знаки отклонений отбрасывают.
Поэтому среднее отклонение dср находят как сумму отклонений без знаков, деленную на число наблюдений n:
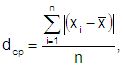
где хi - результаты отдельных наблюдений;
-х - среднее арифметическое.
В большинстве случаев этого уравнения достаточно для характеристики воспроизводимости результатов анализа.
Чем меньше значение dср, тем точнее выполнено определение и тем меньше его результат искажен случайными ошибками.
Но более правильное представление о значении случайных ошибок дает стандартное среднеквадратичное отклонение σ, вычисляемое по уравнению
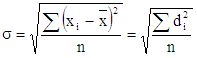 ,
,
Теоретически считается, что при большом числе определений с вероятностью или надежностью α = 0,997 случайная ошибка определений не выйдет за пределы ± 3σ (см. рис. 67).
Установлено, что при большом числе определений результат х, выходящий за пределы ` х ± 3σ, получается только в трех случаях из каждой тысячи определений.
Однако в теории вероятности принято более строгое выражение для характеристики ошибки через так называемое среднее квадратическое отклонение или погрешность отдельного определения S:
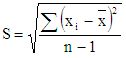 ,
,
Это уравнение точнее, так как в знаменателе подкоренного выражения стоит n-1, что делает невозможным расчет воспроизводимости на основании одного опыта. Кроме того, при возведении в квадрат отрицательные значения отклонений становятся положительными.
Пример. В результате пяти параллельных опытов получены следующие значения содержания примеси магния в известняке (%): 5,24; 5,37; 5,33; 5,38; 5,28.
Решение. Вычисляют среднее арифметическое:
-х = (5,24 + 5,37 + 5,33 + 5,38 + 5,28) / 5 = 5,32%.
Отклонения каждого результата от среднего (%) составляют: -0,08; +0,05; +0,01; +0,06 и -0,04. Поэтому по упрощенному уравнению, отбрасывая знаки отклонений, находят среднее отклонение:
dср = (0,08 + 0,05 + 0,01 + 0,06 + 0,04) / 5 = 0,05%.
Отсюда надежность среднего результата х = 5,32 ± 0,05.
Квадраты величин отдельных отклонений составляют 0,0064; 0,0025; 0,0001; 0,0036; 0,0016. Из них находят среднее квадратическое отклонение определения:
![]()
Из решения следует, что значения ошибок, полученные по упрощенному уравнению, почти совпадают со значениями, вычисленными по уравнению среднего квадратического отклонения. Но значения среднего квадратического отклонения для характеристики ошибки с большей вероятностью являются более надежными для оценок достоверности опыта.
Дисперсионный анализ. Дисперсионный анализ разработан английским ученым Фишером, который открыл закон распределения средних квадратов (дисперсий), т.е. отношение среднего квадрата выборочных объектов к среднему квадрату объектов: S12/ S22 = F.
При дисперсионном анализе одновременно обрабатывают данные нескольких выборок (вариантов), составляющих единый статистический комплекс, оформленный в виде специальной рабочей таблицы.
Сущностью дисперсионного анализа является расчленение общей суммы квадратов отклонений и общего числа степеней свободы на части - компоненты, соответствующие структуре эксперимента, и оценка значимости действия и взаимодействия изучаемых факторов по F-критерию.
Если обрабатывают однофакторные статистические комплексы, состоящие из нескольких независимых выборок, например, С-вариантов в вегетационном опыте, то общая изменчивость результативного признака, измеряемая общей суммой квадратов Сх, расчленяется на два компонента: варьирование между выборками Сv и внутри выборок Cz. В общей форме изменчивость признака может быть представлена выражением: Сх = Сv + Cz.
Здесь вариация между выборками (вариантами) представляет ту часть общей дисперсии, которая обусловлена действием изучаемых факторов, а дисперсия внутри выборок характеризует случайное варьирование изучаемого признака, т.е. ошибку эксперимента.
Общее число степеней свободы (N - 1) также расчленяется на две части - степени свободы для вариантов (t - 1) и для случайного варьирования (N - t) : (N - 1) = (t - 1) + (N - t).
Если обрабатывают однофакторные статистические комплексы, когда выборки (варианты) связаны каким-то общим контролирующим условием например наличием организованных повторений в опыте, общая сумма квадратов разлагается на три части: варьирование повторения Ср, вариантов Сv и случайное Cz. В подобных случаях общая изменчивость и общее число степеней свободы могут быть представлены выражениями:
Сх = Ср + Сv + Cz.
(N -1) = (n - 1) + (t - 1) + (n - 1) (t - 1).
Преимущества дисперсионного анализа перед методом попарных сравнений по критерию Стьюдента:
1) вместо индивидуальных ошибок, средних по каждому варианту, в дисперсионном анализе используется обобщенная ошибка средних, которая опирается на большее число наблюдений, следовательно, является более надежной базой для оценок;
2) методом дисперсионного анализа можно обрабатывать данные простых и сложных, однолетних и многолетних; однофакторных и многофакторных опытов;
3) дисперсионный анализ позволяет избежать громоздких вычислений при большом числе вариантов в опыте и позволяет компактно в виде существенных разностей представить итоги статобработки.