ФИЗИКА

Задача 1.7. На горизонтальной поверхности находится клин массой m2 с углом α. На грань клина кладут брусок массой m1. Найти ускорение клина и силы N и N2, с которыми брусок давит на клин и клин давит на плоскость. Все поверхности соприкасающихся тел считать гладкими.

Решим задачу с применением неинерциальной системы отсчёта.

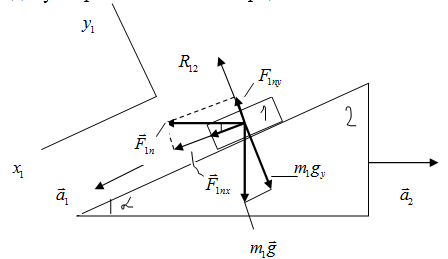
Рис. 1.7.1

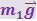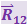Пусть a1 - ускорение бруска в системе отсчёта, связанной с клином. Эта система отсчёта является неинерциальной, так как клин движется относительно Земли (ИСО) с ускорением ax. На брусок кроме сил и , действует сила инерции:

(1.7.1)

.

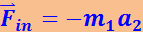Запишем уравнение движения бруска в системе отсчёта, связанной с клином, в векторной форме:

(1.7.2)

.

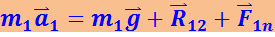В проекциях на оси координат ОХ и ОY  уравнения движения принимают следующий вид:

(1.7.3)

.

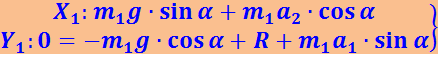Рассматривая движение клина по-прежнему относительно Земли, приходим к следующим уравнениям

(1.7.4)

;

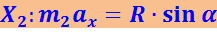(1.7.5)

.

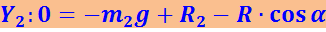Исключая R из уравнений (1.7.3) и (1.7.4), получаем:

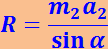
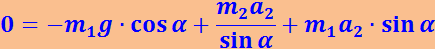
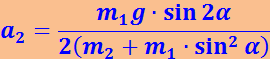
Анализ результатов:

а) пусть m2 >> m1 (очень тяжёлый клин). Тогда, т.е. неподвижен;

б) m1 >> m2 (тяжёлый брусок на очень лёгком клине), 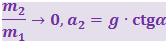. Тяжёлый брусок практически свободно падает с ускорением g и вытесняет клин.

к к к