ФИЗИКА

Задача 5.9. На круглое отверстие радиусом 1 мм в непрозрачном экране падает нормально параллельный пучок света с длиной волны 0,5 мкм. На пути лучей, прошедших через отверстие, помещают экран.

Определить максимальное расстояние от отверстия до экрана, при котором в центре дифракционной картины ещё будет наблюдаться тёмное пятно.

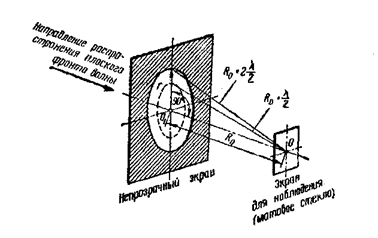
Расстояние, при котором будет видно тёмное пятно, определяется числом зон Френеля, укладывающихся в отверстие. Если число зон чётное, то в центре дифракционной картины будет тёмное пятно.

Число зон Френеля, помещающихся в отверстие, убывает по мере удаления экрана от отверстия. Наименьшее чётное число зон равно 2. Следовательно, максимальное расстояние, при котором ещё будет наблюдаться тёмное пятно в центре экрана, определяется условием, согласно которому в отверстие должно поместиться две зоны Френеля. Согласно рисунка, расстояние от центра экрана О до края отверстия 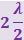больше, чем расстояние от центра экрана до центра отверстия OO1 = R0.

По теореме Пифагора

.

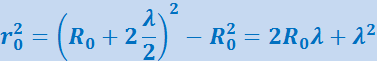Если учесть, что λ<<R0 и что членом, содержащим λ2, можно пренебречь, то это равенство можно переписать в виде

.

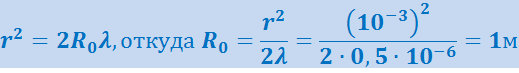к к к