ФИЗИКА
1.4.9. Основное уравнение релятивистской динамики
Как показывает детальное рассмотрение, основное уравнение динамики Ньютона 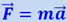 не удовлетворяет принципу относительности Эйнштейна. Чтобы удовлетворить требованиям принципа, основное уравнение динамики должно иметь другой вид и лишь при ν << c переходит в ньютоновское уравнение. Этим требованиям удовлетворяет уравнение
не удовлетворяет принципу относительности Эйнштейна. Чтобы удовлетворить требованиям принципа, основное уравнение динамики должно иметь другой вид и лишь при ν << c переходит в ньютоновское уравнение. Этим требованиям удовлетворяет уравнение
(1.23.1)
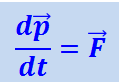 ,
,
где  - сила, действующая на частицу.
- сила, действующая на частицу.
Данное уравнение по виду полностью совпадает с основным уравнением ньютоновской динамики (1.4.5). Однако физический смысл здесь уже другой: слева стоит производная по времени от релятивистского импульса, определяемого формулой (1.22.3).
Подставив (1.22.3) в (1.23.1), запишем последнее уравнение так:
(1.23.2)
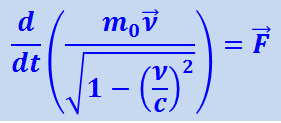
Это и есть основное уравнение релятивистской динамики.
Из него следует неожиданный вывод: вектор ускорения ![]() частицы в общем случае не совпадает по направлению с вектором силы
частицы в общем случае не совпадает по направлению с вектором силы 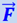 . Покажем это. Для этого запишем (1.22.2) в такой форме:
. Покажем это. Для этого запишем (1.22.2) в такой форме:
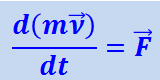 ,
,
где т – релятивистская масса частицы. Выполнив дифференцирование по времени, получим
(1.23.3)
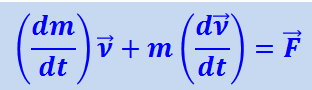 .
.
Это выражение графически представлено на рис. 1.23.1. Таким образом, действительно вектор ускорения ![]() в общем случае не коллинеарен вектору силы
в общем случае не коллинеарен вектору силы 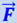 .
.
Рис. 1.23.1 |
Основное уравнение релятивистской динамики позволяет найти закон действующей на частицу силы 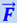 , если известна зависимость от времени релятивистского импульса
, если известна зависимость от времени релятивистского импульса 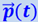 , а с другой стороны, найти уравнение движения частицы
, а с другой стороны, найти уравнение движения частицы 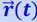 , если известны действующая сила и начальные условия – скорость
, если известны действующая сила и начальные условия – скорость  и положение
и положение  частицы в начальный момент времени.
частицы в начальный момент времени.
к к к