ФИЗИКА
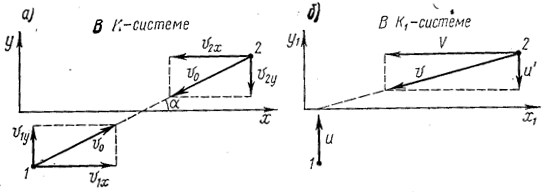
Пусть в некоторой инерциальной K-системе отсчёта навстречу друг другу движутся две одинаковые частицы 1 и 2 с одинаковой скоростью ν0, но под углом α к оси х (рис. 1.22.1). В этой системе отсчёта суммарный импульс обеих частиц, очевидно, сохраняется: до и после столкновения он равен нулю.
Рис. 1.22.1 |
Теперь выясним, как будет обстоять дело в другой инерциальной системе отсчёта. Для этого выберем сначала две системы отсчёта: K1-систему, движущуюся вправо со скоростью ν1x, и K2-систему, движущуюся влево со скоростью ν2x (рис. 1.22.1а). Ясно, что частица 1 в K1-системе и частица 2 в K2-системе движутся только вдоль оси y, причём с одинаковыми по модулю скоростями, которые мы обозначим U.
Рассмотрим картину столкновения в K1-системе (рис. 1.22.1б), где частица 1 имеет скорость U. Найдём y-составляющую скорости частицы 2 в этой системе отсчёта, обозначив её U'. Эта частица движется со скоростью вдоль оси y в K2-системе и, кроме того, вместе с K2-системой перемещается влево со скоростью V относительно K1-системы. Поэтому, согласно (1.19.1), y-составляющая скорости частицы 2 в K1-системе равна закону сохранения, независимо от выбора инерциальной системы отсчёта
(1.22.1)
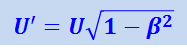 .
.
Запишем теперь y-составляющие импульсов обеих частиц в K1-системе: m1U и m2U'. Согласно (1.22.1), U' < U, поэтому закон сохранения импульса в ньютоновской формулировке не выполняется. Действительно, в нашем случае m1=m2 и, следовательно, y-составляющая суммарного импульса частиц до столкновения отлична от нуля, а после столкновения равна нулю.
Возникает альтернатива: отказаться или от ньютоновского определения импульса, или от закона сохранения этой величины.
Учитывая громадную роль, которую играют законы сохранения, в теории относительности за фундаментальный принимают именно закон сохранения импульса и уже отсюда находят выражения для самого импульса.
С учётом этого потребуем, чтобы закон сохранения импульса выполнялся и в K1-системе, т.е. положим, что m1U1=m2U'. Отсюда, с учётом (1.22.1), получим
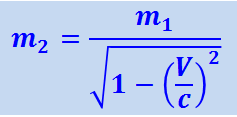 .
.
При α → 0 (рис. 1.21.1) U → 0 и m1 представляет собой массу покоящейся частицы; её обозначают m0 и называют массой покоя. Скорость же V при этом условии оказывается равной ν – скорости частицы 2 относительно частицы 1. Поэтому последнюю формулу можно переписать так:
(1.22.2)
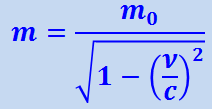 ,
,
где т – масса движущейся частицы.
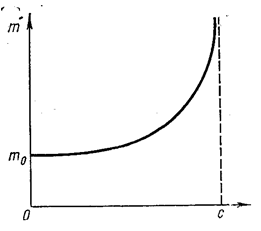
Её называют релятивистской. Они больше массы покоя и зависят от скорости частицы (рис. 1.22.2). Другими словами, масса одной и той же частицы различна в разных инерциальных системах отсчёта.
Рис. 1.21.2 |
В отличии от релятивистской массы масса покоя частицы m0 - величина инвариантная, т.е. одинаковая во всех системах отсчёта. По этой причине можно утверждать, что именно масса покоя является характеристикой частицы.
Сделаем последний шаг – напишем выражение для импульса релятивистской частицы:
(1.22.3)
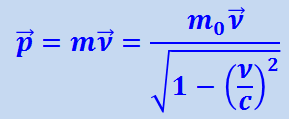 .
.
Это и есть так называемый релятивистский импульс частицы. Опыт подтверждает, что так определённый импульс действительно подчиняется закону сохранения независимо от выбора инерциальной системы отсчёта.
к к к