ФИЗИКА
Теперь нам предстоит решить фундаментальный вопрос о формулах преобразования координат и времени при переходе от одной инерциальной системы отсчёта к другой.
Преобразования Галилея? Напомним, что эти преобразования основаны на предположениях, что длина тел не зависит от движения и время течёт одинаково в различных инерциальных системах отсчёта. Однако в предыдущем разделе было показано, что в действительности это не так: течение времени и длина тел зависят от системы отсчёта – выводы, являющиеся неизбежным следствием постулатов Эйнштейна. Поэтому мы вынуждены отказаться от преобразований Галилея, или, говоря точнее, признать, что они – лишь частный случай каких-то более общих преобразований.
Возникает задача отыскания таких формул преобразования, которые, во-первых, учитывали бы замедление времени и лоренцово сокращение (т.е. были бы, в конечном счёте, следствиями постулатов Эйнштейна), и, во-вторых, переходили бы в предельном случае малых скоростей в преобразования Галилея. Перейдём к решению этой задачи.
Рассмотрим две инерциальные системы отсчёта K и K'. Пусть K'-система движется относительно K-системы со скоростью 
. Направим координатные оси обеих систем отсчёта так, как показано на рис. 1.18.1: оси x и x' совпадают и направлены параллельно вектору 
, а оси y и y' параллельны друг другу. Установим в разных точках обеих систем отсчёта одинаковые часы и синхронизируем их – отдельно часы K-системы и отдельно часы K'-системы. И наконец, возьмём за начало отсчёта времени в обеих системах момент, когда начала координат О и О' совпадают (t = t' = 0).
Рис. 1.18.1 |
Предположим теперь, что в момент времени t (в K-системе) в точке с координатами x, y произошло некоторое событие А, например, вспыхнула лампочка. Наша задача – найти координаты x', y' и момент времени t' этого события в K'-системе.
Вопрос о координате y' был уже решён ранее y' = y. Поэтому перейдём к нахождению координаты x'. Координата x' характеризует собственную длину отрезка O'P, неподвижного в K'-системе (рис. 1.18.1). Длина же этого отрезка в K-системе, где отсчёт производится в момент t, равна x - νt. Связь между этими длинами даётся формулой (1.17.3), согласно которой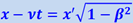 
. Отсюда
(1.18.1)
.
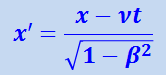С другой стороны, координата x характеризует собственную длину отрезка ОР, неподвижного в K-системе. Длина же этого отрезка в K'-системе, где измерение производится в момент t', равна x' + νt'. Учитывая (1.17.3), получим
,
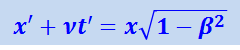откуда
(1.18.2)
.
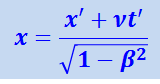Полученные формулы позволяют также установить и связь между моментами времени t и t' события А в обеих системах отсчёта. Для этого достаточно исключить из (1.18.1) и (1.18.2) x' или x, после чего найдём
(1.18.3)
.
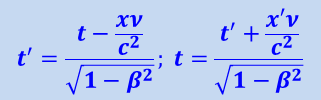Формулы (1.18.1), (1.18.2) и (1.18.3) называют преобразованиями Лоренца. Они играют фундаментальную роль в теории относительности. По этим формулам осуществляется преобразование координат и времени любого события при переходе от одной инерциальной системы к другой.
Итак, преобразования Лоренца при переходе от K-системы к K'-системе имеют вид:
(1.18.4)
,
а при обратном переходе от K' к K-системе:
(1.18.5)
,
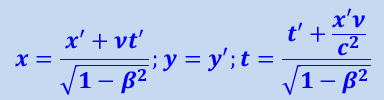где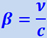 
, ν - скорость K'-системы относительно K-системы.
Преобразования Лоренца сильно отличаются от преобразований Галилея (1.3.3), однако последние могут быть получены из (1.18.4) и (1.18.5), если в них формально положить c = ∞. Что это значит?
Ранее было отмечено, что в основе преобразований Галилея лежит допущение о синхронизации часов с помощью мгновенно распространяющихся сигналов. Из этого следует, что величина с в преобразованиях Лоренца играет роль скорости тех сигналов, которые используют для синхронизации часов. Если эта скорость бесконечна велика, то получаются преобразования Галилея; если же она равна скорости света, то – преобразования Лоренца. Таким образом, в основе преобразований Лоренца лежит допущение о синхронизации часов с помощью световых сигналов, имеющих предельную скорость.
Особенностью преобразований Лоренца является то, что при ν << c они переходят в преобразования Галилея. Это означает, что теория относительности не отвергает преобразований Галилея как неправильные, но включает их в истинные законы преобразования как частный случай, справедливый при ν << c. В дальнейшем мы увидим, что это отражает общую взаимосвязь между теорией относительности и ньютоновской механикой – законы и соотношения теории относительности переходят в законы ньютоновской механики в предельном случае малых скоростей.
Далее из преобразований Лоренца следует, что при ν > c подкоренные выражения становятся отрицательными. Это соответствует тому факту, что движение тел со скоростью, большей скорости света в вакууме, невозможно.
Нельзя даже пользоваться системой отсчёта, движущейся со скоростью ν = c; при этом подкоренные выражения обращаются в нуль. Это значит, что, например, с фотоном, движущимся со скоростью с, принципиально не может быть связана система отсчёта. Или иначе: не существует такой системы отсчёта, в которой фотон был бы неподвижным.
Наконец, необходимо обратить внимание на то, что в формулы преобразования времени входит пространственная координата. Это указывает на неразрывную связь между пространством и временем. Другими словами, речь должна идти не отдельно о пространстве и времени, а о едином пространстве – времени, в котором протекают все физические явления.
к к к