ФИЗИКА

1.4.3. Замедление времени и сокращение длины

Рассмотрим три важнейших следствия, которые вытекают из постулатов Эйнштейна, – это равенство поперечных размеров движущихся тел в разных системах отсчёта, замедление хода движущихся часов и сокращение продольных размеров движущихся тел.

Приступая к решению этих вопросов, напомним, прежде всего, что под системой отсчёта подразумевается тело отсчёта, с которым связаны координатная сетка и ряд неподвижных одинаковых часов, синхронизированных между собой. Кроме того будем полагать, что системы отсчёта являются инерциальными, и что координатные сетки и часы в них проградуированы одинаковым образом.

1. Равенство поперечных размеров тел. Начнём с вопроса о сравнении поперечных размеров тел в разных инерциальных системах отсчёта. Пусть имеем две инерциальные системы отсчёта К и К’, оси y и y’, которые параллельны друг другу и перпендикулярны направлению движения одной системы относительно другой (рис. 1.17.1), причём начало отсчёта О’K’-системы движется по прямой, проходящей через начало отсчёта ОК-системы. Установим вдоль осей y и y’ стержни ОА и О’A’, являющиеся эталонами метра в каждой из этих систем отсчёта. Представим себе далее, что в момент совпадения осей y’ и y верхний конец левого стержня сделает метку на оси у К-системы. Совпадёт ли эта метка с точкой А – верхним концом правого стержня?

Принцип относительности позволяет сразу ответить на этот вопрос: да, совпадёт. Если бы это было не так, то с точки зрения обеих систем отсчёта один из стержней оказался бы, например, короче другого и, следовательно, имелась бы возможность экспериментально отличить одну из инерциальных систем отсчёта от другой по более коротким поперечным размерам. Однако это противоречит принципу относительности.

Отсюда следует, что поперечные размеры тел одинаковы во всех инерциальных системах отсчёта. Это означает, что при указанном выборе начал отсчёта K' и K-систем координаты y’ и y любой точки или события совпадают, т.е.

.

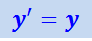Это соотношение представляет собой одно из искомых преобразований координат.

2. Замедление времени. Наша следующая задача – сравнить течение времени в разных инерциальных системах отсчёта. Как уже отмечалось, время измеряется часами, причём под часами имеется в виду любой прибор, в котором используется тот или иной периодический процесс. Поэтому в теории относительности принято обычно говорить о сравнении хода идентичных часов в разных инерциальных системах отсчёта.

Наиболее просто этот вопрос можно решить с помощью следующего мысленного (т.е. в принципе возможного) эксперимента. Возьмём так называемые световые часы – стержень с зеркалами на обоих концах, между которыми «бегает» короткий световой импульс. Период таких часов равен интервалу времени между двумя последовательными моментами, когда световой импульс достигает какого-то определённого конца стержня.

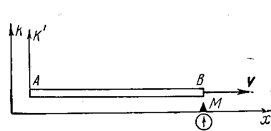
Далее представим себе две инерциальные системы отсчёта K' и K, движущиеся относительно друг друга со скоростью ν. Пусть световые часы АВ неподвижны в K'-системе и ориентированы перпендикулярно направлению её движения относительно K-системы (рис. 1.17.2). Проследим теперь за «ходом» этих часов в обеих системах отсчёта.

В K'-системе часы неподвижны, и их период

,

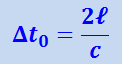где ℓ - расстояние между зеркалами, c - скорость света.

В K-системе относительно которой часы движутся, расстояние между зеркалами также ℓ, так как поперечные размеры тел одинаковы в разных инерциальных системах отсчёта. Однако путь светового импульса в этой системе отсчёта будет уже иным – зигзагообразным (рис. 1.17.2). Пока световой импульс распространяется от нижнего зеркала к верхнему, последнее переместится на некоторое расстояние вправо и т.д.

Поэтому световой импульс, чтобы вернуться к нижнему зеркалу, проходит в K-системе больший путь, причём с той же скоростью с. Значит свету понадобится на это больше времени – больше, чем когда часы неподвижны. Другими словами период движущихся часов удлинится – с точки зрения K-системы они будут идти медленнее.

Обозначим период движущихся часов через Δt в K-системе. Из прямоугольного треугольника AB'A' (рис. 1.17.2) следует, что

,

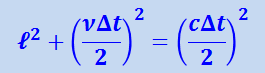откуда

.

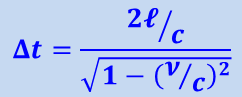А так как 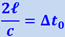, то

(1.17.2)

,

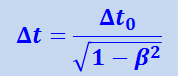где 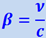, ν - скорость часов в K-системе.

Отсюда видно, что Δt > Δt0, т.е. одни и те же часы в разных инерциальных системах отсчёта идут по-разному: в той системе отсчёта, относительно которой часы движутся, они идут медленнее, чем в системе отсчёта, где они покоятся. Другими словами, движущиеся часы идут медленнее, чем покоящиеся. Это явление называют замедлением времени.

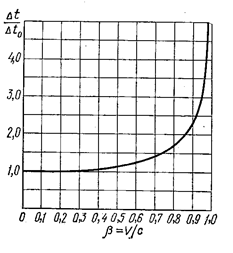
Время, отсчитываемое по часам, движущимся вместе с телом, в котором происходит какой-либо процесс, называют собственным временем этого тела. Его обозначают Δt0. Как следует из (1.17.2), собственное время самое короткое. Время Δt того же процесса в другой системе отсчёта зависит от скорости ν этой системы относительно тела, в котором происходит процесс. Эта зависимость особенно сильно проявляется для значений скорости ν, сравнимых со скоростью света (рис. 1.17.3).

Таким образом, в отличие от ньютоновской механики течение времени в действительности зависит от состояния движения. Не существует единого мирового времени, и понятие «промежуток времени между двумя событиями» оказывается относительным. Утверждение, что между двумя данными событиями прошло столько-то секунд, приобретает смысл только тогда, когда указано, к какой системе отсчёта это утверждение относится.

Абсолютное время ньютоновской механики является в теории относительности приближённым понятием, справедливым только при малых (по сравнению со скоростью света) относительных скоростях систем отсчёта. Это сразу следует из (1.17.2) и видно из рис. 1.17.3: при ν << c Δt ≈ Δt0.

Итак, мы пришли к фундаментальному выводу: время в системе отсчёта, движущейся с часами, течёт медленнее (для наблюдателя относительно которого эти часы движутся). Это же относится и ко всем процессам, протекающим в движущихся относительно наблюдателя системах отсчёта.

Естественно возникает вопрос: заметит ли наблюдатель в K'-системе, движущей относительно K-системы, что его часы идут медленнее, чем часы K-системы? Нет, не заметит. Это сразу же следует из принципа относительности. Если бы K'-наблюдатель тоже обнаружил замедление времени в своей системе отсчёта, то это означало бы, что для обоих наблюдателей K' и K - время течёт медленнее в одной из инерциальных систем отсчёта. Из этого они заключили бы, что одна из инерциальных систем отсчёта отличается от другой – в противоречии с принципом относительности.

Отсюда следует, что эффект замедления времени является взаимным, симметричным относительно обеих инерциальных систем отсчёта K и K'. Иначе говоря, если с точки зрения K-системы медленнее идут часы K'-системы, то с точки зрения K'-системы, наоборот, медленнее идут часы K-системы (причём в том же отношении). Это обстоятельство указывает на то, что явление замедления времени является чисто кинематическим. Оно представляет собой обязательное следствие инвариантности скорости света и никак не может быть приписано какому-либо изменению в свойствах часов, обусловленному их движением.

Формула (1.17.2) сразу же нашла экспериментальное подтверждение, объяснив «загадочное» на первый взгляд поведение мюонов при прохождении земной атмосферы. Мюоны – это нестабильные частицы, которые самопроизвольно распадаются в среднем через 2 ⋅ 10-6 c (это время измерено в условиях, когда они неподвижны или движутся с малыми скоростями). Мюоны образуются в верхних слоях атмосферы на высоте 20-30 км. Если бы время жизни мюонов не зависело от их скорости, то, двигаясь даже со скоростью света, они не могли бы проходить путь больше, чем

.

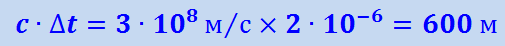Однако наблюдения показывают, что значительное число мюонов всё-таки достигает земной поверхности. Это объясняется тем, что время 2 ⋅ 10-6 c - это собственное время (Δt0), жизни мюонов, т.е. время по часам, движущимся вместе с мюонами. Время же по земным часам должно быть согласно (1.17.2), гораздо больше (скорость этих частиц близка к скорости света) и оказывается достаточным, чтобы мюоны могли достигнуть поверхности Земли.

В заключение несколько слов о так называемом «парадоксе часов», или парадоксе близнецов». Пусть имеются двое одинаковых часов А и В, из которых часы А неподвижны в некоторой инерциальной системе отсчёта, а часы В сначала удаляются от часов А, а затем возвращаются к ним. Предполагается, что в начальный момент, когда часы находились вместе, они показывали одно и то же время.

С «точки зрения» часов А движущимися являются часы В, поэтому они идут медленнее и по возвращении отстанут от часов А. С «точки же зрения» часов В, наоборот, движутся часы А, поэтому по возвращении отстанут именно они. Явное противоречие – в этом суть «парадокса».

В действительности в этих рассуждениях допущена принципиальная ошибка. Эта ошибка касается рассуждения с «точки зрения» часов В, ибо система отсчёта, связанная с этими часами является неинерциальной (она сначала удаляется с ускорением, а затем приближается), и мы не имеем права в данном случае использовать результаты, относящиеся только к инерциальным системам отсчёта. Детальный расчёт, выходящий за рамки специальной теории относительности, показывает, что часы, движущиеся с ускорением (в нашем случае часы В), идут медленнее, поэтому при возвращении отстанут именно они.

3. Лоренцово сокращение. Пусть стержень АВ движется относительно K-системы отсчёта с постоянной скоростью ν (рис. 1.17.4) и длина стержня равна ℓ0 в системе отсчёта, связанной со стержнем. Наша задача – определить длину ℓ данного стержня в K-системе.

Проведём для этого следующий мысленный эксперимент. Сделаем на оси х K-системы метку М и установим около неё часы. Зафиксируем по этим часам время пролёта Δt0 стержня мимо метки М. Тогда можно утверждать, что искомая длина стержня в K-системе

.

Для наблюдателя, связанного со стержнем, время пролёта будет иным. Действительно, для него часы, показавшие пролётное время Δt0 движутся со скоростью , а значит, показывают «чужое» время. «Своё» время пролёта Δt для этого наблюдателя будет, согласно (1.17.2), больше. Это время он может найти из соотношения

.

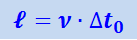Из последних двух уравнений, с учётом (1.17.2), получим

,

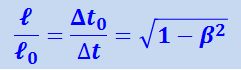или

(1.17.3)

,

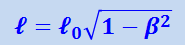где .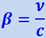

Длину ℓ0, измеренную в системе отсчёта, где стержень неподвижен, называют собственной длиной.

Таким образом, продольный размер движущегося стержня оказывается меньше его собственной длины, т.е. ℓ < ℓ0. Это явление называют лоренцовым сокращением. Сравнительно с формой тела в системе отсчёта, где оно покоится, его форма в движущейся системе отсчёта может характеризоваться как сплющенная в направлении движения.

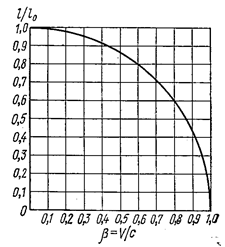
Из формулы (1.17.3) следует, что степень сокращения зависит от скорости ν. Эта зависимость особенно существенно проявляется для значений скорости ν, сравнимых со скоростью света (рис. 1.17.5)

Итак, в разных инерциальных системах отсчёта длина одного и того же стержня оказывается различной. При скоростях же ν << c  ℓ ≈ ℓ0 и длина тела приобретает практически абсолютный смысл.

Необходимо отметить, что лоренцово сокращение, как и замедление времени, должно быть взаимным. Значит, лоренцово сокращение является также чисто кинематическим эффектом – в теле не возникает каких-либо напряжений, вызывающих деформацию.

Итак, понятия длины и промежутка времени столь же относительны, как понятия движения и покоя.

к к к