ФИЗИКА
На основе анализа экспериментального и теоретического материала Эйнштейном была создана специальная теория относительности. Термин «специальная» говорит о том, что она относится только к инерциальным системам отсчёта.
Эта теория принимает без изменения такие положения ньютоновской механики, как евклидовость пространства и закон инерции Галилея-Ньютона.
В качестве исходных позиций специальной теории относительности Эйнштейн принял два постулата:
1) принцип относительности,
2) независимость скорости света от скорости источника.
Первый постулат представляет собой обобщение принципа относительности Галилея на любые физические процессы:
все физические явления протекают одинаковым образом во всех инерциальных системах отсчёта; все законы природы и уравнения, их описывающие, инвариантны, т.е. не меняются, при переходе от одной инерциальной системы отсчёта к другой.
Другими словами, все инерциальные системы отсчёта эквивалентны (неразличимы) по своим физическим свойствам; никаким опытом нельзя в принципе выделить ни одну из них как предпочтительную.
Второй постулат утверждает, что скорость света в вакууме не зависит от движения источника света и одинакова во всех направлениях.
Это значит, что скорость света в вакууме одинакова во всех инерциальных системах отсчёта.
Как мы увидим, наличие такой скорости существенно изменяет представления о пространстве и времени.
Из постулатов Эйнштейна следует также, что скорость света в вакууме является предельной. Именно предельный характер этой скорости и объясняет одинаковость скорости света во всех системах отсчёта, иначе эти системы можно было бы отличить друг от друга.
Наличие предельной скорости автоматически предполагает ограничение скорости движения частиц величиной с.
Таким образом, согласно постулатам Эйнштейна, значение всех возможных в природе скоростей движения тел и распространения взаимодействий ограничено величиной с. Этим самым отвергается принцип дальнодействия ньютоновской механики.
Синхронизация часов. По Эйнштейну физической реальностью обладает не точка пространства и не момент времени, когда что-либо произошло, а только само событие. Для описания события в данной системе отсчёта нужно указать место, в котором оно происходит, и момент времени, когда оно происходит.
Положение точки, в которой происходит событие, может быть определено с помощью жёстких масштабов методами евклидовой геометрии и выражено в декартовых координатах.
Соответствующий же момент времени можно определить с помощью часов, помещённых в ту точку системы отсчёта, где происходит данное событие.
Если же нам надо сравнить время в различных точках системы отсчёта, то надо обеспечить синхронный ход всех часов данной системы.
Ясно, что синхронизировать часы можно только с помощью каких-нибудь сигналов. Наиболее быстрые сигналы, пригодные для этой цели – световые или радиосигналы, распространяющиеся с известной скоростью с. Выбор именно этих сигналов обусловлен ещё и тем, что их скорость не зависит от направления распространения в пространстве, а также одинакова во всех инерциальных системах отсчёта.
Далее можно поступить следующим образом. Наблюдатель, находящийся, например, в начале координат О данной системы отсчёта, сообщает по радио: «Передаём сигнал точного времени. Сейчас по моим часам время t0». В момент, когда этот сигнал достигнет часов, находящихся на известном расстоянии r от точки О, их устанавливают так, чтобы они показывали время t = t0 + r/c, т.е. с учётом времени запаздывания сигнала. В результате такой операции можно утверждать, что все часы данной системы отсчёта показывают в каждый момент одно и то же общее время. Существенно отметить, что определённое таким образом время относится лишь к той системе отсчёта, относительно которой синхронизированные часы покоятся.
Соотношения между событиями. Обратимся к вопросу о пространственных и временных соотношениях между данными событиями в разных инерциальных системах отсчёта.
Уже в ньютоновской механике пространственные соотношения между различными событиями зависят от того, к какой системе отсчёта они относятся. Например, две последовательные вспышки лампочки в движущимся поезде происходят в одной и той же точке системы отсчёта, связанной с поездом, но в разных точках системы отсчёта, связанной с полотном дороги.
В противоположность этому временные соотношения между событиями в ньютоновской механике считаются не зависящими от системы отсчёта. Это значит, что если какие-нибудь два события происходят одновременно в одной системе отсчёта, то они являются одновременными и во всех других системах отсчёта.
Легко, однако, убедиться, что в действительности это не так – одновременность (а, следовательно, и течение времени) является понятием относительным, приобретающим смысл только тогда, когда указано, к какой системе отсчёта это понятие относится.
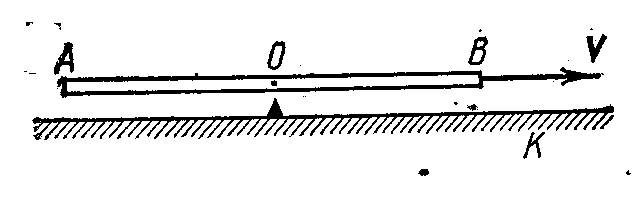
Пусть имеем стержень АВ, движущийся с постоянной скоростью v относительно К-системы отсчёта. В середине стержня находится лампочка О, по концам – в точках А и В – фотоэлементы (рис. 1.16.1). Пусть в некоторый момент лампочка О дала кратковременную вспышку света. Поскольку скорость распространения света в системе отсчёта, связанной со стержнем, равна с в обоих направлениях, то световые импульсы достигнут равноудалённых от О фотоэлементов А и В в один и тот же момент времени и оба фотоэлемента сработают одновременно.
Рис. 1.16.1 |
Иначе обстоит дело в К-системе. В этой системе отсчёта скорость световых импульсов в обоих направлениях также равна с, однако проходимые ими пути различны. Действительно, пока световые импульсы идут к точкам А и В, последние переместятся вправо и, следовательно, фотоэлемент А сработает раньше фотоэлемента В.
Таким образом, события, одновременные в одной системе отсчёта, не являются одновременными в другой системе отсчёта, т.е. одновременность в отличии от представлений ньютоновской механики является понятием относительным. А это в свою очередь означает, что время в разных системах отсчёта течёт неодинаково.
Если бы в нашем распоряжении имелись мгновенно распространяющиеся сигналы, то события одновременные в одной системе отсчёта, были бы одновременными и в любой другой системе. Однако таких сигналов в действительности нет.
к к к