Для того чтобы описать поведение фирмы, необходимо знать, какое количество продукта она может произвести, используя ресурсы в тех или иных объемах.

Исходным пунктом такого анализа служит производственная функция. Она была разработана в 1890 г. английским математиком А. Берри, помогавшим А. Маршаллу при подготовке математического приложения к работе «Принципы экономической науки».

Производственная функция во многом похожа на функцию полезности в теории потребления. Это объясняется тем, что по отношению к ресурсам фирма является потребителем и производственная функция характеризует именно эту сторону производства – производство как потребление.

1. Существует предел увеличения объема производства, который может быть достигнут увеличением затрат одного ресурса при прочих равных условиях. Это значит, что на фирме при данном количестве станков и производственных помещений есть предел увеличения производства посредством привлечения большего количества рабочих. Прирост выпуска при увеличении численности занятых будет приближаться к нулю.

2. Существует определенная взаимодополняемость (комплементарностъ) факторов производства, но без сокращения объема производства возможна и определенная взаимозаменяемость этих факторов. Например, эффективен труд работников, если они обеспечены всеми необходимыми орудиями труда. При отсутствии таких орудий объем может быть сокращен или увеличен при росте численности занятых. В данном случае происходит замена одного ресурса другим.

3. Способ производства А считается технически более эффективным по сравнению со способом В, если он предполагает использование хотя бы одного ресурса в меньшем, а всех остальных – не в большем количестве, чем способ В. Технически неэффективные способы не используются рациональными производителями.

4. Если способ А предполагает использование одних ресурсов в большем, а других – в меньшем количестве, чем способ В, эти способы несравнимы по их технической эффективности. В этом случае оба способа считаются технически эффективными и включаются в производственную функцию. Какой из них выбрать – зависит от соотношения цен применяемых ресурсов. Этот выбор основывается на критериях экономической эффективности. Следовательно, техническая эффективность не тождественна экономической эффективности.

В теории производства традиционно используется 2-факторная производственная функция, в которой объем производства является функцией использованных ресурсов труда и капитала:

Q = f (L, K).

Графически каждый способ производства (технология) может быть представлен точкой, характеризующей минимальный необходимый набор двух факторов, нужных для производства данного объема продукции (рис. 20).

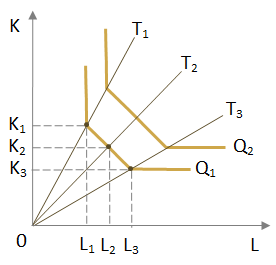
Рис. 20. Технология и производственная функция

Эти сочетания ресурсов (технологии) являются наиболее эффективными, так как любая точка на изокванте соответствует минимальным объемам ресурсов, необходимым для получения заданного объема готовой продукции.

Изокванта обычно выпукла к началу координат вследствие предполагающейся взаимозаменяемости ресурсов. Когда ресурсы являются взаимодополняемыми, изокванта имеет L-образную форму. Когда ресурсы представляют собой совершенные субституты, кривая принимает форму прямой линии.

Совокупность изоквант, отражающая максимально достижимый выпуск продукции при любом заданном наборе факторов производства, называется картой изоквант.

В долгосрочном периоде, когда фирма может изменять все факторы производства, действует принцип экономии от масштаба. Если вместе с ростом затрат факторов производства происходит пропорциональное увеличение выпуска продукции, наблюдается постоянная отдача от масштаба. Если выпуск увеличивается в меньшей степени, чем объемы используемых ресурсов, имеет место убывающая отдача от масштаба. При обратной пропорции наблюдается возрастающая отдача.

В краткосрочном периоде, когда один фактор производства переменный, а другой – постоянный, расширение производства подчиняется закону убывающей производительности (отдачи) переменного фактора. В современной экономической науке общепризнано, что закон убывающей производительности носит всеобщий характер и относится к любой человеческой деятельности, основанной на использовании двух или более факторов, и количество одного из них непрерывно увеличивается, а другого (других) остается неизменным.

Если любое сочетание двух ресурсов можно приобрести за одну и ту же сумму, то математическим выражением зависимости выпуска от затраченных ресурсов служит уравнение равных затрат (изокоста). Оно аналогично бюджетной линии потребителя, но относится к приобретению ресурсов фирмой. Точка касания изокосты и изокванты определяет наименьшую стоимость ресурсов при заданном объеме производства. В этом случае производитель находится в равновесном состоянии.