Экологический мониторинг и экологическая экспертиза

2.4. Баланс кислорода в атмосфере
Для нахождения критических воздействий, за пределами которых возможны нарушения сложившихся в биосфере биогеохимических циклов необходимо проследить за балансом основных химических элементов и их соединений. Необходимо установить нарушения в этих балансах, выяснить тенденции этих нарушений, определить пути их устранения.
Соответствующие решения основываются на использовании балансовой модели (Горстко, Сурков, 1975).
В общем виде эта модель описывается уравнением
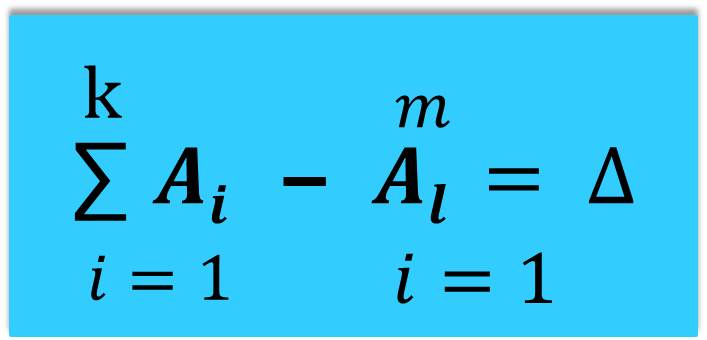
где Аi – приходные статьи баланса;
Аl – расходные статьи баланса;
∆ – сальдо (разность между приходной и расходной статьями).
Допустим, что рассматривается баланс кислорода в атмосфере.
Если ∆ = 0, баланс кислорода в атмосфере имеет место.
Если ∆ > 0, приходная часть превосходит расходную и (кислород в атмосфере накапливается).
Если ∆ < 0, то расходная часть превышает приходную и (количество кислорода в атмосфере уменьшается).
Такая тенденция прослеживается в действительности.
Систематическое превышение расходной части баланса кислорода над приходной может привести к нежелательным последствиям. |
Масштабная антропогенная деятельность, уничтожение лесов и естественной растительности, загрязнение океана промышленными и другими отходами сокращают приходную часть баланса. Расширение химических и иных производств, строительство тепловых электростанций, использование двигателей внутреннего сгорания приводят к увеличению расходной статьи баланса.
Балансовые соотношения позволяют уловить тенденции в степени антропогенного воздействия на круговороты веществ. Но они не несут в себе достаточной информации о нарушениях равновесия биосферы. Даже при удовлетворительном состоянии глобального баланса могут наблюдаться нарушения, как в отдельных биогеоценозах, так и в их группах. Вмешательство человека в природу требует изучения балансов в динамике.
Для описания динамики используют дифференциальные уравнения, которые характеризуют скорости изменения составляющих приходной и расходной части баланса Аi и Аl:
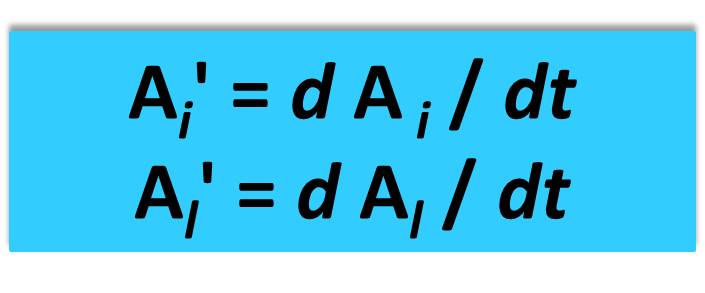
Учитывают также зависимость этих скоростей от внешних и внутренних факторов.
Вектор Ā включает в себя компоненты приходной и расходной частей баланса (А = A1, А2, ... , Аn), а также внешние факторы U, влияющие на скорости изменения вектора Ā (в частности, воздействия со стороны человека).
Вектор внешних воздействий будет Ū = (U1, U2, ... , Um).
С учетом сказанного, систему изучаемых дифференциальных уравнений можно представить в виде
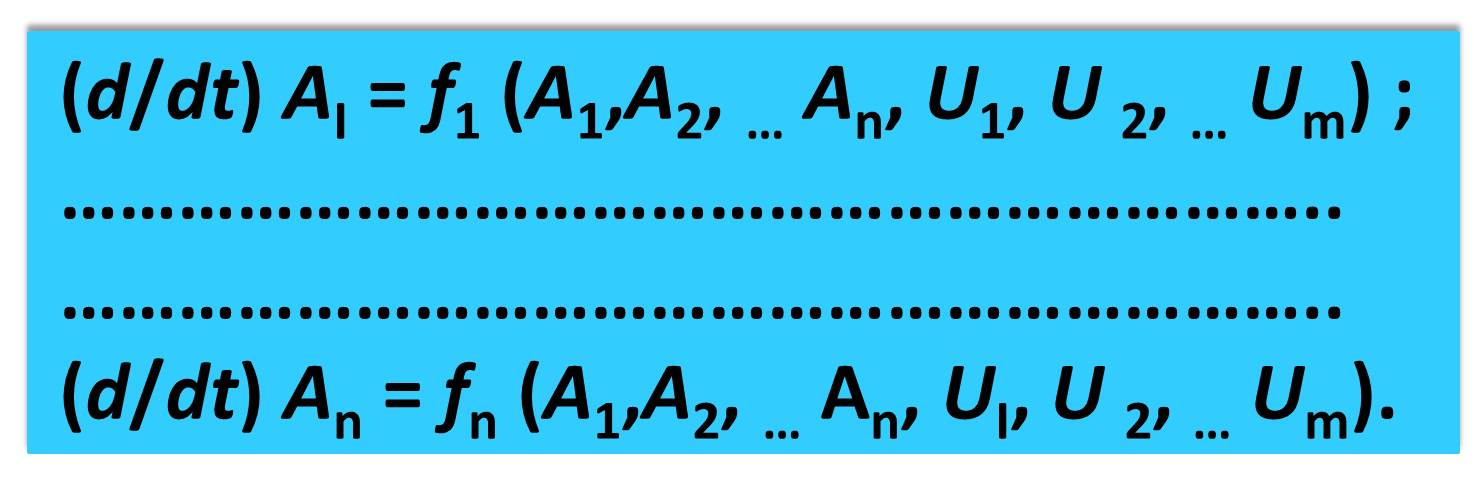
Скорость изменения (производную по времени) интересующей нас величины
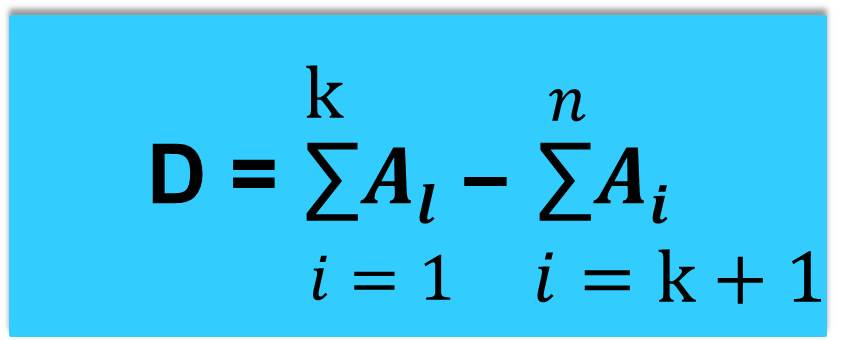
можно представить через правые части вышеприведенных дифференциальных уравнений.
Тогда она будет
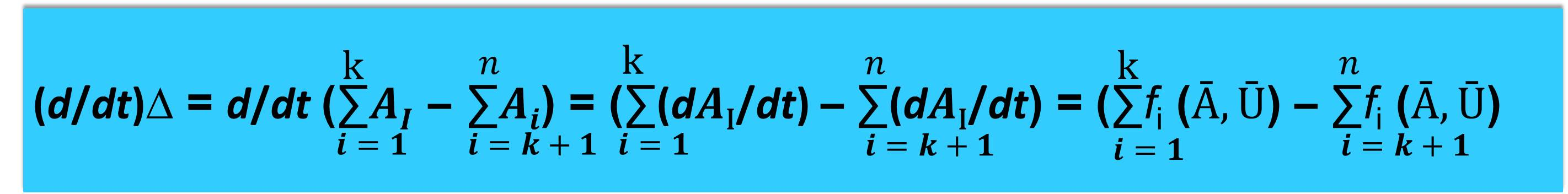
Из приведенного уравнения можно получить явное выражение для изменения баланса во времени — для ∆(t):
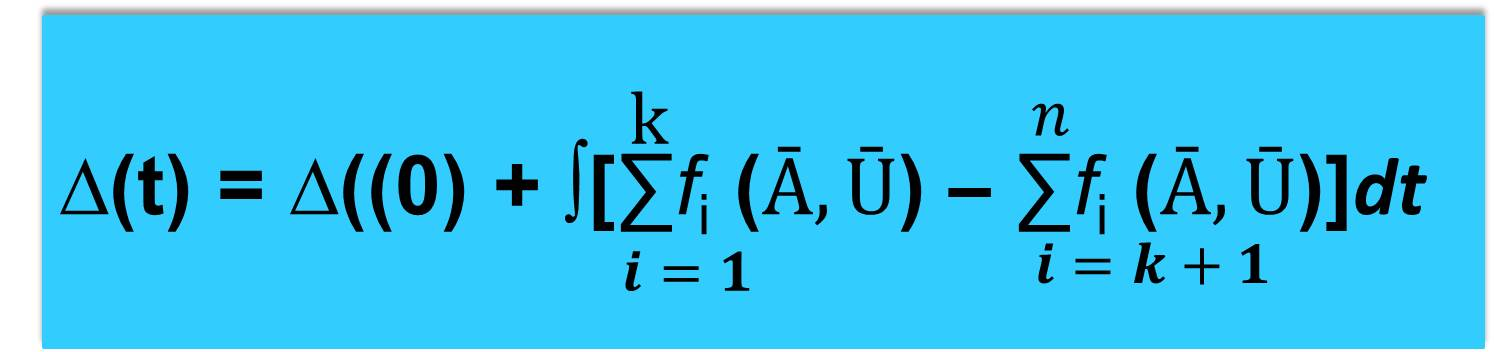
Если известны значения каждой из компонент вектора Ā в любой момент времени t, то можно судить о закономерности изменения величины ∆(t).
Построив график поведения каждой из компонент Аi вектора Ā, получим фазовое пространство, в котором выполняются балансы.
Введя ограничения для тех компонент вектора Ā, приходная часть баланса которых не может превышать расходную, устанавливаем критическую область фазового пространства. Попадание в эту область свидетельствует о том, что изменение величин баланса превосходит некоторое допустимое критическое значение.
Предположительно, функции, находящиеся в правой части уравнений, известны. О виде этих функций правомерно судить лишь отчасти: по характеру поведения всей системы. Сделать предположения об особенностях поведения изученных некоторых характеристик экосистем реально, вводя в анализ функции, посредством аппарата математического моделирования. Важно, чтобы модель была тождественной проблеме, возникшей и изучаемой в заданной системе.
