ФИЗИКА

3.5.12. Эффект Холла

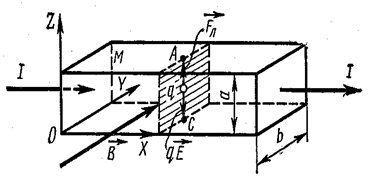
Американский физик Э. Холл проделал следующий опыт. Он пропускал постоянный электрический ток I через золотую пластинку М (рис. 3.5.26) и измерял разность потенциалов между противолежащими точками А и С на верхней и нижней гранях. Эти точки лежат в одном и том же поперечном сечении проводника М. Поэтому, как следовало ожидать, оказалось, что . Когда пластина с током была помещена в однородное магнитное поле, перпендикулярное к её боковым граням, то потенциалы точек А и С стали различными. Это явление получило название эффекта Холла. Оказалось, что разность потенциалов между точками А и С прямо пропорциональна силе тока I, индукции магнитного поля В и обратно пропорциональна ширине пластинки b, т.е.

(3.5.75)

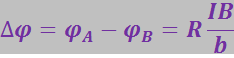
где R – константа Холла.

Дальнейшие исследования показали, что явление Холла наблюдается во всех проводниках и полупроводниках независимо от их материала. Изменение направления тока или направления магнитного поля на противоположное вызывает изменение знака разности потенциалов . Величина константы Холла R зависит от материала пластинки М, причём этот коэффициент для одних веществ положителен, а для других – отрицателен.

Эффект Холла можно объяснить следующим образом. Пусть ток I в пластинке М обусловлен упорядоченным движением электрических зарядов q. Если число этих зарядов в единице объёма пластинки равно , а средняя скорость их упорядоченного движения равна , то сила тока выразится формулой:

(3.5.76)

где – площадь поперечного сечения пластинки.

Если заряды q положительны, то их скорость совпадает с направлением тока, и в формуле (3.5.76) ν > 0. Если же заряды q отрицательны, то их скорость противоположна направлению тока, и в формуле (3.5.76) ν < 0.

На заряд q, движущийся в магнитном поле с индукцией , действует магнитная сила , равная

(3.5.77)

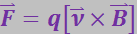
Под влиянием этой силы заряды отклоняются к верхней грани пластинки (это справедливо только для изображённых на рис. 3.5.26 направлений тока и вектора ). Таким образом, вблизи верхней грани будет избыток зарядов q, а вблизи нижней грани обнаружится их недостаток. В результате этого в пластине возникает поперечное электрическое поле, направленное сверху вниз, если заряды q положительны, и снизу вверх , если они отрицательны. Обозначим напряжённость образовавшегося электрического поля через . Сила , действующая со стороны поперечного электрического поля на заряд q, направлена в сторону, противоположную направлению магнитной силы . В случае равновесного процесса прохождения тока по пластине эти силы взаимно уравновешиваются, т.е.

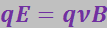
откуда

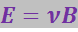
Если пластинка М достаточно длинная и широкая, то поперечное электрическое поле в ней можно считать однородным (оно подобно полю в плоском конденсаторе). Тогда разность потенциалов между точками А и С равна:

Заменив ν его выражением из (3.5.76), получим:

(3.5.78)

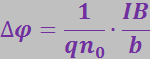
Полученный результат совпадает с экспериментальной формулой (3.5.75). Из сравнения (3.5.78) и (3.5.75) следует, что

(3.5.79)

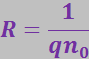
Из формулы (3.5.79) видно, что знак константы Холла совпадает со знаком заряда q носителей тока. Поэтому на основании измерения константы Холла для полупроводника можно судить о природе его проводимости.

При электронной проводимости R < 0, а при дырочной – R > 0. Если в полупроводнике одновременно осуществляют оба типа проводимости, то по знаку константы Холла можно судить о том, какой из них является преобладающим.

Можно также с помощью константы Холла определить концентрацию носителей тока, если характер проводимости и заряд носителей тока известен (например, для металлов), а именно:

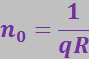
Так для одновалентных металлов оказалось, что концентрация электронов проводимости совпадает с концентрацией атомов.

к к к