ФИЗИКА
3.5.11. Движение заряженных частиц в однородном магнитном поле
Начнём с простейшего случая – движения заряженной частицы вдоль линий индукции магнитного поля. При таком движении частицы угол α между векторами её скорости ![]() и индукции
и индукции ![]() равен 0 или π. Поэтому по формуле (3.5.39) магнитная сила равна нулю, т.е. магнитное поле не действует на частицу. Она будет двигаться по инерции – равномерно и прямолинейно.
равен 0 или π. Поэтому по формуле (3.5.39) магнитная сила равна нулю, т.е. магнитное поле не действует на частицу. Она будет двигаться по инерции – равномерно и прямолинейно.
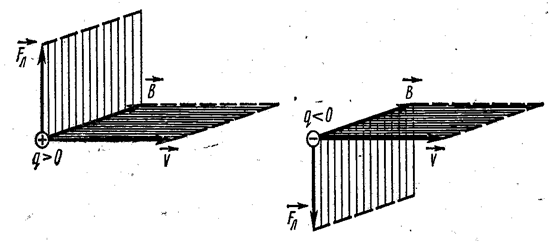
Пусть теперь частица, имеющая заряд q, движется перпендикулярно к линиям магнитной индукции (α = π/2). Тогда магнитная сила равна
(5.65)
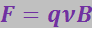
и направлена перпендикулярно векторам ![]() и
и ![]() (рис. 3.5.22). Следовательно, частица движется в плоскости, перпендикулярной к вектору магнитной индукции, причём сила F является центростремительной силой
(рис. 3.5.22). Следовательно, частица движется в плоскости, перпендикулярной к вектору магнитной индукции, причём сила F является центростремительной силой ![]() :
:
(3.5.66)
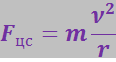
где т – масса заряженной частицы, а r – радиус кривизны её траектории.
Рис. 3.5.22 |
Приравняв правые части (3.5.65) и (3.5.66), найдём радиус кривизны траектории
(3.5.67)
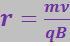
Так как в однородном поле B = const, а численное значение скорости заряда в магнитном поле не изменяется, то радиус кривизны траектории этого заряда оказывается постоянным. Поэтому заряженная частица будет двигаться по окружности, плоскость которой перпендикулярна к магнитному полю, а радиус прямо пропорционален скорости частицы и обратно пропорционален произведению её удельного заряда q/m на индукцию В поля.
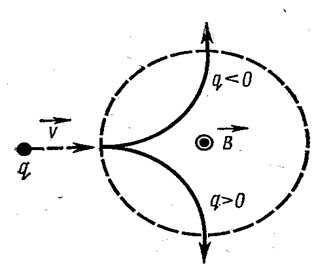
Направление магнитной силы и направление вызываемого ею отклонения заряженной частицы в магнитном поле зависит от знака заряда q частицы. Если частица движется в плоскости чертежа (рис. 3.5.23) слева направо, а магнитное поле направлено из-за чертежа перпендикулярно к его плоскости, то при q > 0 частица отклоняется вниз, а при q < 0 – вверх. Таким образом, по характеру отклонения частицы в магнитном поле можно судить о знаке её заряда. Этим широко пользуются в исследованиях элементарных частиц.
Рис. 3.5.23 |
Частица движется по окружности равномерно, поэтому период её обращения определяется соотношением:
(3.5.68)

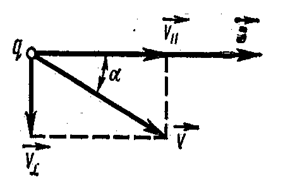
Рассмотрим теперь общий случай движения заряженной частицы в однородном магнитном поле, когда её скорость ![]() направлена под произвольным углом α к вектору индукции поля
направлена под произвольным углом α к вектору индукции поля ![]() (рис. 3.5.24).
(рис. 3.5.24).
Рис. 3.5.24 |
Разложим вектор скорости ![]() на две составляющие: параллельную вектору
на две составляющие: параллельную вектору ![]()
![]() и перпендикулярную к нему
и перпендикулярную к нему ![]() :
:
(3.5.69)
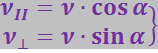
Скорость ![]() в магнитном поле не изменяется. Благодаря же скорости
в магнитном поле не изменяется. Благодаря же скорости ![]() частица должна двигаться по окружности, плоскость которой перпендикулярна вектору
частица должна двигаться по окружности, плоскость которой перпендикулярна вектору ![]() , а радиус по формуле (3.5.67) равен:
, а радиус по формуле (3.5.67) равен:
(3.5.70)
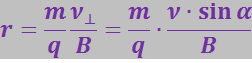
Частица одновременно участвует в двух движениях: она равномерно вращается со скоростью ![]() по окружности радиуса r и движется поступательно с постоянной скоростью
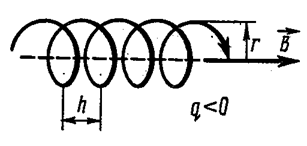
по окружности радиуса r и движется поступательно с постоянной скоростью ![]() в направлении, перпендикулярном к плоскости вращения. Поэтому траектория движения заряженной частицы представляет собой винтовую линию, ось которой совпадает с линией индукции магнитного поля (рис. 3.5.25). Радиус витков r выражается формулой (3.5.70), а расстояние h между соседними витками (шаг винтовой линии) равно:
в направлении, перпендикулярном к плоскости вращения. Поэтому траектория движения заряженной частицы представляет собой винтовую линию, ось которой совпадает с линией индукции магнитного поля (рис. 3.5.25). Радиус витков r выражается формулой (3.5.70), а расстояние h между соседними витками (шаг винтовой линии) равно:
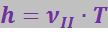
Рис. 3.5.25 |
Заменив Т по формуле (3.5.68), а ![]() по (3.5.69), получим:
по (3.5.69), получим:
(3.5.71)
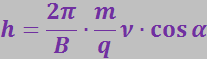
Формулы (3.5.67) и (3.5.68) получены, исходя из ньютоновского уравнения ![]() . Иначе обстоит дело в релятивистском случае. Поскольку магнитная сила перпендикулярна к скорости частицы, модуль остаётся постоянным. Поэтому уравнение:
. Иначе обстоит дело в релятивистском случае. Поскольку магнитная сила перпендикулярна к скорости частицы, модуль остаётся постоянным. Поэтому уравнение:

упрощается следующим образом:
(3.5.72)
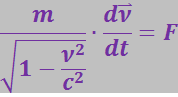
![]() .
.
В этом уравнении ![]() есть нормальное ускорение
есть нормальное ускорение ![]() , модуль которого равен
, модуль которого равен ![]() . Модуль силы в данном случае
. Модуль силы в данном случае ![]() . Заменив в (3.5.72) векторы их модулями, получим уравнение:
. Заменив в (3.5.72) векторы их модулями, получим уравнение:
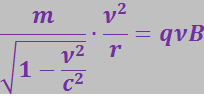
откуда
(3.5.73)
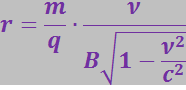
Следовательно, для периода обращения частицы ![]() получается формула:
получается формула:
(3.5.74)
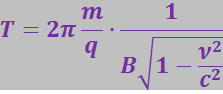
Таким образом, в релятивистском случае период обращения по мере увеличения скорости уменьшается. При ν << c (3.5.74) переходит в (3.5.68).
Из предыдущего следует, что траекторию заряженных частиц можно формировать с помощью магнитного поля. Этот способ широко используется во всех современных ускорителях.
к к к