ФИЗИКА

3.5.10. Работа, совершаемая при перемещении проводника с током в магнитном поле

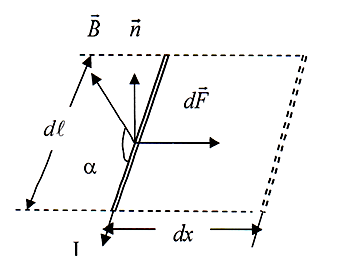
На проводнике с током в магнитном поле действуют силы Ампера. Вычислим работу dA, совершаемую этими силами при перемещении элемента проводника с током I в магнитном поле. Для простоты предположим, что элемент проводника перемещается в направлении действующей на него силы (рис. 3.5.20).

В этом случае работа dA равна произведению численных значений силы и перемещения :

(3.5.58)

По закону Ампера (3.5.37):

Подставив это выражение в (3.5.58), получим:

(3.5.59)

Сила и перемещение направлены перпендикулярно элементу проводника . Следовательно, произведение представляет собой площадь поверхности, описанной элементом проводника при его перемещении на расстояние .

Из рис. 3.5.20 видно, что

,

где – проекция вектора на направление нормали к площади dS.

Произведение равно магнитному потоку сквозь поверхность dS. Поэтому формулу (3.5.59) можно переписать в виде:

(3.5.60)

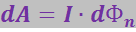
Полагая силу тока постоянной и интегрируя это выражение, получим:

(3.5.61)

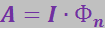
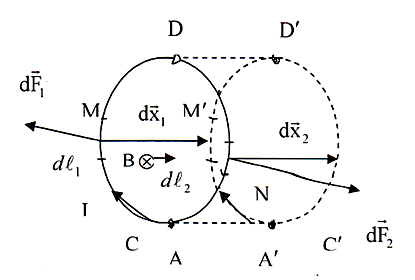
Найдём выражение для работы, совершаемой силами Ампера при перемещении в магнитном поле замкнутого контура С, по которому проходит постоянный ток I (рис. 3.5.21).

Пусть в результате бесконечно малого перемещения контур С занял положение C', изображённое на рис. 3.5.21 пунктиром. Контур С разобьём мысленно на два соединённых своими концами проводника АМD и DNA. Полная работа dA, совершаемая силами Ампера при рассматриваемом перемещении контура, равна алгебраической сумме работ перемещения проводников AMD(dA1) и DNA(dA2), т.е.

(3.5.62)

Предположим, что вектор магнитной индукции направлен перпендикулярно к плоскости чертежа так, что линии индукции уходят за чертёж. В таком случае сила Ампера , действующая на произвольный элемент проводника DNA, составляет острый угол с направлением его перемещения и совершает положительную работу. Наоборот, сила , действующая на элемент проводника АМD, составляет с направлением его перемещения тупой угол и совершает отрицательную работу. Поэтому работы dA1 и dA2 перемещения проводников АМD и DNA имеют разные знаки (dA1 < 0, dA2 > 0). Для получения абсолютных значений работ dA1 и dA2 необходимо продифференцировать выражение (3.5.61). Поэтому уравнение (3.5.62) можно записать в виде:

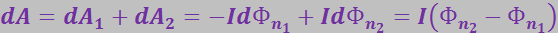
где – изменение магнитного потока, пронизывающего поверхность, ограниченную контуром, при перемещении контура из положения С в положение C'.

Таким образом, окончательное выражение для элементарной работы dA будет

(3.5.63)

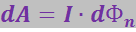
Интегрируя это выражение, найдём работу А, совершаемую силами Ампера при любом перемещении контура в магнитном поле:

(3.5.64)

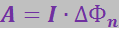
Работа по перемещению проводников с током в магнитном поле совершается теми источниками, которые создают в них постоянный электрический ток.

к к к