ФИЗИКА

3.5.9. Контур с током в магнитном поле

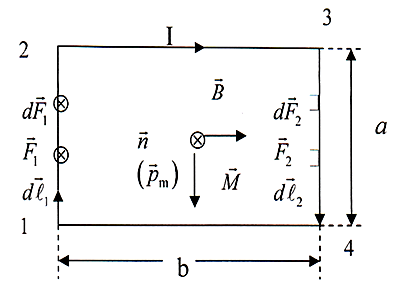
Рассмотрим, как ведёт себя контур с током в магнитном поле. При этом ограничимся рассмотрением плоских контуров. Вычислим результирующий вращающий момент, создаваемый силами (3.5.36), приложенными к контуру, изображённому на рис. 3.5.17. Сначала будем считать поле однородным.

Из рисунка видно, что прямоугольный контур ориентирован так, что вектор параллелен двум из его сторон. При указанных направлениях тока и поля на каждый элемент участка 1-2 действует направленная за чертёж сила , модуль которой равен , а на каждый элемент участка 3-4 действует направленная «на нас» сила , модуль которой равен . Участки 2-3 и 4-1 параллельны полю, поэтому силы на них не действуют.

Результирующая сил приложена к середине участка 1-2 и имеет модуль, равный . Аналогично результирующая сил приложена к середине участка 3-4 и имеет модуль такой же величины, что и . Силы и образуют пару сил с плечом, равным b. Следовательно, на контур действует вращающий момент:

где S – площадь контура. Учтя взаимную ориентацию векторов , и орта нормали , можно написать, что

(3.5.51)

Выражение в круглых скобках представляет собой магнитный момент контура (см. 3.5.30).

Таким образом, приходим к формуле:

(3.5.52)

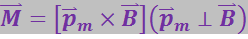
Можно доказать, что формулы (3.5.51) и (3.5.52) справедливы для плоских контуров любой формы, находящихся в однородном магнитном поле.

В случае, когда векторы и коллинеарны, силы, действующие на отдельные элементы контура, лежат в одной плоскости (плоскости контура) и, следовательно, не могут обусловить вращающий момент. Эти силы стремятся растянуть (если и имеют одинаковое направление) либо сжать (если и имеют противоположные направления) контур.

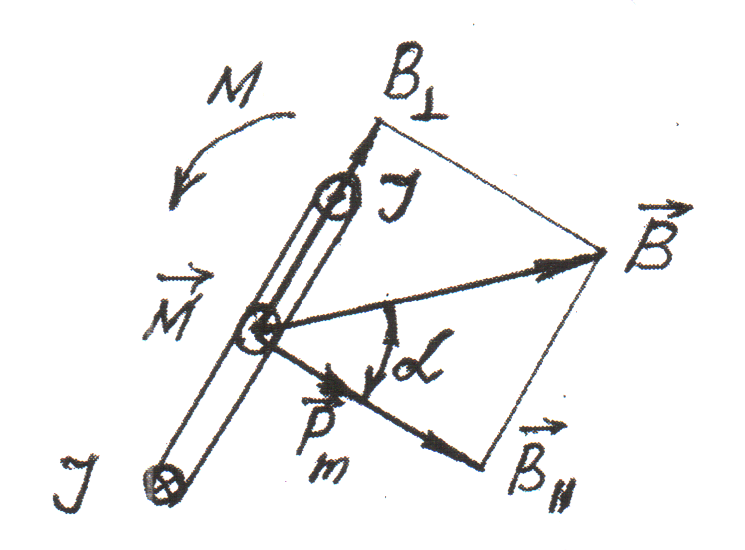
Рассмотрим случай, когда и образуют произвольный угол α (рис. 3.5.18).

Разложим магнитную индукцию на две составляющие: – параллельную и – перпендикулярную к вектору , и рассмотрим действие каждой составляющей отдельно. Составляющая будет обуславливать силы, растягивающие или сжимающие контур. Составляющая , имеющая модуль , приведёт к возникновению вращающего момента, который можно вычислить по (3.5.52):

(3.5.53)

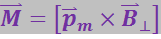
Поскольку , то (3.5.53) можно записать в виде:

(3.5.54)

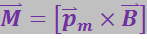
Модуль вектора равен:

(3.5.55)

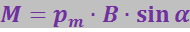
где α – угол между векторами и .

Для того, чтобы этот угол увеличить на , нужно совершить работу против сил, действующих на контур в магнитном поле

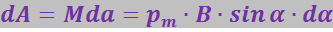
Эта работа идёт на увеличение потенциальной энергии , которой обладает контур с током в магнитном поле,

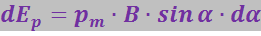
Интегрируя, найдём, что

Если положить , то

(3.5.56)

Параллельная ориентация векторов и соответствует минимуму энергии (3.5.56) и, следовательно, положению устойчивого равновесия.

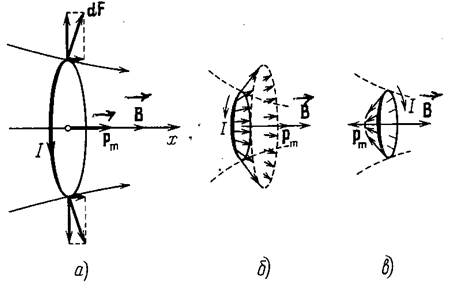
Рассмотрим далее поведение плоского кругового контура с током, находящегося в неоднородном осесимметричном магнитном поле. Ось симметрии поля обозначим буквой х. Контур расположим так, чтобы его центр оказался на оси х, а магнитный момент контура был ориентирован по полю (рис. 3.5.19).

Поскольку , то на каждый элемент контура действует сила , перпендикулярная к , т.е. к линии магнитной индукции в месте её пересечения с . Поэтому силы, приложенные к различным элементам контура, образуют симметричный конический веер (рис. 3.5.19б).

Их результирующая сила направлена в сторону возрастания и, следовательно, втягивает контур в область более сильного поля. Если изменить направление тока на обратное (при этом станет противоположным ), направления всех сил и их результирующей изменятся на обратные (рис. 3.5.19в) и контур будет выталкиваться из поля.

С помощью (3.5.56) можно легко найти модуль силы . Если ориентация магнитного момента по отношению к полю остаётся неизменной (α = const), то будет зависеть только от х. Продифференцировав (3.5.56) по х и изменив у результата знак на обратный, получим проекцию силы на ось х:

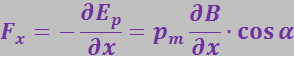
В силу осевой симметрии поля можно считать, что . Тогда

(3.5.57)

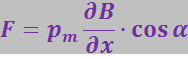
к к к