ФИЗИКА
3.5.8. Поток и циркуляция вектора магнитной индукции
В природе нет магнитных зарядов, вследствие чего линии ![]() не имеют ни начала, ни конца – они либо замкнуты, либо уходят в бесконечность. Поэтому в соответствии с формулой (3.1.24) поток
не имеют ни начала, ни конца – они либо замкнуты, либо уходят в бесконечность. Поэтому в соответствии с формулой (3.1.24) поток ![]() вектора
вектора ![]() через замкнутую поверхность должен быть равен нулю. Следовательно, для любого магнитного и произвольной замкнутой поверхности S:
через замкнутую поверхность должен быть равен нулю. Следовательно, для любого магнитного и произвольной замкнутой поверхности S:
(3.5.41)

Эта формула выражает теорему Гаусса для вектора ![]() : поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.
: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.
Отсутствие начала и конца магнитных линий означает, что дивергенция вектора ![]() всюду равна нулю:
всюду равна нулю:
(3.5.42)
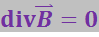
Найдём циркуляцию вектора ![]() . По определению циркуляция равна интегралу
. По определению циркуляция равна интегралу
(3.5.43)
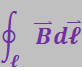
где ![]() – элемент замкнутого контура, по которому производится интегрирование.
– элемент замкнутого контура, по которому производится интегрирование.
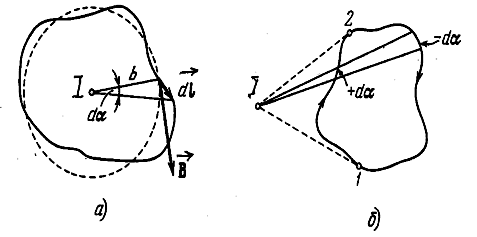
Проще всего вычислить интеграл (3.5.43) в случае прямого тока. Пусть замкнутый контур лежит в плоскости перпендикулярной к проводу, по которому за чертёж течёт ток I (рис. 3.5.10). В каждой точке контура вектор ![]() направлен по касательной к окружности, проходящей через эту точку. Представим
направлен по касательной к окружности, проходящей через эту точку. Представим ![]() в виде
в виде ![]() (
(![]() – проекция
– проекция ![]() на направление вектора
на направление вектора ![]() ).
).
Из рисунка следует, что ![]() равна bdα, где b – расстояние от провода с током до
равна bdα, где b – расстояние от провода с током до 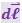 , dα – угол, на который поворачивается радиальная прямая при перемещении вдоль контура на отрезок
, dα – угол, на который поворачивается радиальная прямая при перемещении вдоль контура на отрезок ![]() . Подставив в (3.5.43) это значение
. Подставив в (3.5.43) это значение ![]() и выражение (3.5.27) для В, получим:
и выражение (3.5.27) для В, получим:
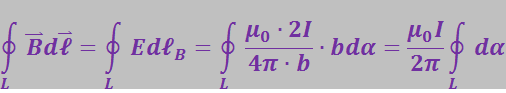
Рис. 5.10 |
При обходе по контуру, охватывающему ток (рис. 3.5.10а), радиальная прямая всё время поворачивается в одном направлении, поэтому ![]() . Если ток не охватывается контуром (рис. 3.5.10б), то радиальная прямая поворачивается сначала в одном направлении (участок 1-2), а затем в противоположном (участок 2-1). Углы dα, отвечающие поворотом в противоположные стороны, отличаются знаком. Поэтому
. Если ток не охватывается контуром (рис. 3.5.10б), то радиальная прямая поворачивается сначала в одном направлении (участок 1-2), а затем в противоположном (участок 2-1). Углы dα, отвечающие поворотом в противоположные стороны, отличаются знаком. Поэтому ![]() . Оба результата можно выразить формулой
. Оба результата можно выразить формулой
(3.5.44)
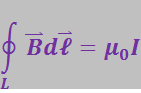
где I – ток, охватываемый контуром.
Если контур тока не охватывает, то I = 0 и циркуляция также равна нулю.
Знак циркуляции зависит от направления обхода по контуру. Его можно учесть, полагая I алгебраической величиной, причём положительным нужно считать ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления будет отрицательным.
Мы получили формулу (3.5.44) для прямого тока и плоского контура. Однако можно доказать, что эта формула справедлива и для неплоского контура, охватывающего ток, текущий по проводу произвольной формы.
Теперь допустим, что контур произвольной формы охватывает несколько проводов с токами. В силу принципа суперпозиции
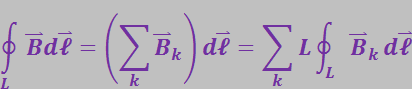
Каждый из интегралов в этой сумме равен ![]() . Следовательно,
. Следовательно,
(3.5.45)
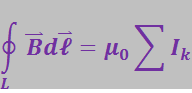
Таким образом, циркуляция вектора ![]() по некоторому контуру равна алгебраической сумме токов, охватываемых контуром, умноженной на
по некоторому контуру равна алгебраической сумме токов, охватываемых контуром, умноженной на ![]() . Это утверждение называется теоремой о циркуляции (или законом полного тока).
. Это утверждение называется теоремой о циркуляции (или законом полного тока).
Поле, у которого циркуляция отлична от нуля, называется вихревым или соленоидальным.
Таким образом, в то время как электростатическое поле потенциально, магнитное поле, в отличие от него, является вихревым.
Применим формулу (3.5.44) для вычисления полей соленоида и тороида.
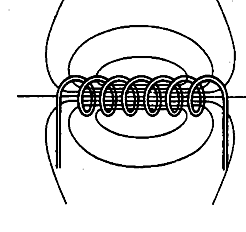
Соленоид представляет собой провод, навитый на круглый цилиндрический каркас. Линии ![]() поля соленоида выглядят примерно так, как показано на рис. 3.5.11. Внутри соленоида направление этих линий образует с направлением тока в витках правовинтовую систему.
поля соленоида выглядят примерно так, как показано на рис. 3.5.11. Внутри соленоида направление этих линий образует с направлением тока в витках правовинтовую систему.
Рис. 3.5.11 |
У реального соленоида имеется составляющая тока вдоль оси. Кроме того, линейная плотность тока ![]() (равная отношению силы тока dI) изменяется периодически при перемещении вдоль соленоида. Среднее значение этой плотности равно:
(равная отношению силы тока dI) изменяется периодически при перемещении вдоль соленоида. Среднее значение этой плотности равно:
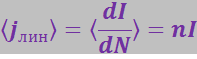 ,
,
где n – число витков соленоида, приходящееся на единицу его длины;
I – сила тока в соленоиде.
Введём в рассмотрение воображаемый бесконечно длинный соленоид. У него отсутствует осевая составляющая тока и линейная плотность тока постоянна по всей длине. Поле такого соленоида однородно и ограничено объёмом соленоида (аналогично электрическое поле бесконечного плоского конденсатора однородно и ограничено объёмом конденсатора).
В соответствии со сказанным представим соленоид в виде бесконечного тонкостенного цилиндра, обтекаемого током постоянной линейной плотности:
(3.5.46)
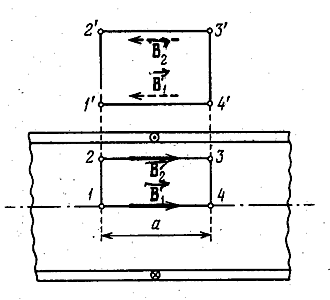
Разобьём цилиндр на одинаковые круговые токи – «витки». Из рис. 3.5.12 видно, что каждая пара витков, расположенных симметрично относительно некоторой плоскости, перпендикулярной к оси соленоида, создаёт в любой точке этой плоскости магнитную индукцию, параллельную оси. Следовательно, и результирующее поле в любой точке внутри и вне бесконечного соленоида может иметь лишь направление, параллельное оси.
Из рис. 3.5.11 вытекает, что направления поля внутри и вне конечного соленоида противоположны. При увеличении длины соленоида направления полей не изменяются и в пределе при ![]() остаются противоположными. Для бесконечного соленоида, как и для конечного, направление поля внутри соленоида образует с направлением обтекания цилиндра током правовинтовую систему.
остаются противоположными. Для бесконечного соленоида, как и для конечного, направление поля внутри соленоида образует с направлением обтекания цилиндра током правовинтовую систему.
Рис. 3.5.12 |
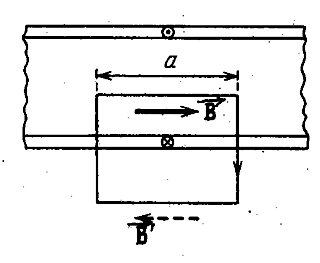
Из параллельности вектора ![]() оси вытекает, что поле как внутри, так и вне бесконечного соленоида должно быть однородным. Чтобы доказать это, возьмём внутри соленоида воображаемый прямоугольный контур 1-2-3-4 (рис. 3.5.13, участок 4-1 идёт по оси соленоида).
оси вытекает, что поле как внутри, так и вне бесконечного соленоида должно быть однородным. Чтобы доказать это, возьмём внутри соленоида воображаемый прямоугольный контур 1-2-3-4 (рис. 3.5.13, участок 4-1 идёт по оси соленоида).
Рис. 3.5.13 |
Обойдя контур по часовой стрелке, получим для циркуляции вектора ![]() значение
значение ![]() . Контур не охватывает токов, поэтому циркуляция должна быть равна нулю. Отсюда следует, что
. Контур не охватывает токов, поэтому циркуляция должна быть равна нулю. Отсюда следует, что ![]() . Располагая участок 2-3 на любом расстоянии от оси, мы каждый раз будем получать, что магнитная индукция
. Располагая участок 2-3 на любом расстоянии от оси, мы каждый раз будем получать, что магнитная индукция ![]() на этом расстоянии равна индукции
на этом расстоянии равна индукции ![]() на оси соленоида. Отсюда следует, что поле внутри соленоида однородно.
на оси соленоида. Отсюда следует, что поле внутри соленоида однородно.
Обратимся к контуру ![]() . Этот контур так же не охватывает токов, поэтому циркуляция вектора
. Этот контур так же не охватывает токов, поэтому циркуляция вектора ![]() , равная
, равная ![]() должна быть равна нулю. Отсюда вытекает, что
должна быть равна нулю. Отсюда вытекает, что ![]() . Расстояния от оси соленоида до участков
. Расстояния от оси соленоида до участков ![]() и
и ![]() были взяты произвольно. Следовательно, значение
были взяты произвольно. Следовательно, значение ![]() на любом расстоянии от оси будет вне соленоида одно и то же, т.е. поле вне соленоида будет однородным.
на любом расстоянии от оси будет вне соленоида одно и то же, т.е. поле вне соленоида будет однородным.
Циркуляция по контуру, изображённому на рис. 3.5.14 равна ![]() . Этот контур охватывает положительный ток величины jлин⋅ а. В соответствии с (3.5.44) должно выполняться равенство:
. Этот контур охватывает положительный ток величины jлин⋅ а. В соответствии с (3.5.44) должно выполняться равенство:

или после сокращения на а и замены ![]() (см. 3.5.46):
(см. 3.5.46):
(3.5.47)
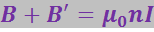
Из этого равенства следует, что поле как внутри, так и снаружи бесконечного соленоида является конечным.
Рис. 3.5.14 |
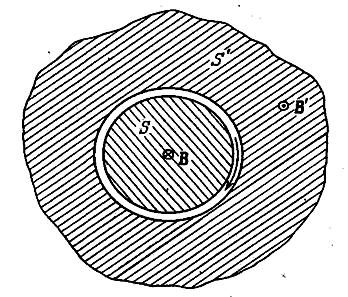
Возьмём плоскость, перпендикулярную к оси соленоида (рис. 3.5.15). Вследствие замкнутости линий ![]() магнитные потоки через внутреннюю часть S этой плоскости и через внешнюю часть S' должны быть одинаковыми. Поскольку поля однородны и перпендикулярны к плоскости, каждый из потоков равен произведению и площади, пронизываемой потоком
магнитные потоки через внутреннюю часть S этой плоскости и через внешнюю часть S' должны быть одинаковыми. Поскольку поля однородны и перпендикулярны к плоскости, каждый из потоков равен произведению и площади, пронизываемой потоком

Рис. 3.5.15 |
Левая часть этого равенства конечна, множитель S' в правой части бесконечен. Отсюда следует, что B' = 0. Положив в (3.5.46) B' = 0, придём к формуле для магнитной индукции внутри соленоида:
(3.5.48)
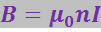
В магнитную индукцию на оси соленоида симметрично расположенные витки вносят одинаковый вклад. Поэтому у конца полубесконечного соленоида на его оси магнитная индукция равна половине значения (3.5.48):
(3.5.49)
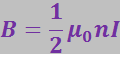
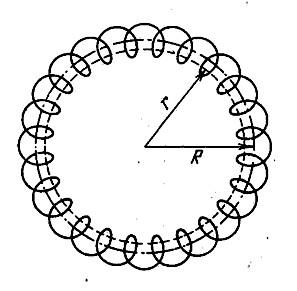
Тороид представляет собой провод, навитый на каркас, имеющий форму тора (рис. 3.5.16). Возьмём контур в виде окружности радиуса r, центр которой совпадает с центром тороида.
Рис. 3.5.16 |
В силу симметрии вектор ![]() в каждой точке должен быть направлен по касательной к контуру. Следовательно, циркуляция
в каждой точке должен быть направлен по касательной к контуру. Следовательно, циркуляция ![]() равна:
равна:

(В – магнитная индукция в тех точках, где проходит контур).
Если контур проходит внутри тороида, он охватывает ток ![]() (R – радиус тороида; n – число витков на единицу его длины). В этом случае
(R – радиус тороида; n – число витков на единицу его длины). В этом случае
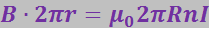
откуда
(3.5.50)
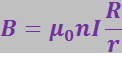
Контур, проходящий вне тороида, токов не охватывает, поэтому для него ![]() . Таким образом, вне тороида магнитная индукция равна нулю.
. Таким образом, вне тороида магнитная индукция равна нулю.
к к к