ФИЗИКА
3.5.7. Закон Ампера. Сила Лоренца
Согласно закону, установленному Ампером, на элемент тока в магнитном поле действует сила
(3.5.36)
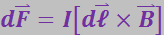
(I – сила тока; 
– магнитная индукция в том месте, где помещается элемент 
).
Модуль этой силы определяется выражением:
(3.5.37)
где α – угол между векторами 
и 
.
Направление силы определяется по правилу правого винта.
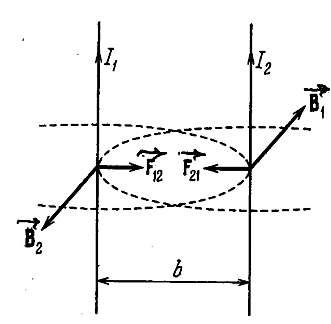
Воспользуемся формулой (3.5.37) для вычисления силы взаимодействия двух находящихся в вакууме параллельных бесконечно длинных прямых токов. Если расстояние между токами b (рис. 3.5.8), то каждый элемент тока I2 будет находиться в возбуждаемом током I1 поле, магнитная индукция которого равна:
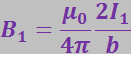
Рис. 3.5.8 |
Угол α между элементами тока I2 и вектором 
прямой. Следовательно, согласно (3.5.37) на элемент тока I2 будет действовать сила:
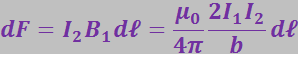
а на единицу длины тока I2 – сила:
(3.5.38)
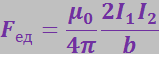
Для силы, действующей на единицу длины тока I1, получается такое же выражение.
Легко убедиться в том, что при изображённом на рис. 3.5.8 направлении токов они отталкивают друг друга.
На основании формулы (3.5.38) устанавливается единица силы тока в СИ – ампер. Ампер определяется как сила неизменяющегося тока, который, проходя по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызвал бы между этими проводниками силу, равную 
на каждый метр длины.
Если точечный заряд q движется со скоростью v в магнитном поле, то как показывает эксперимент, в точке поля, где магнитная индукция равна 
, на него будет действовать сила:
(3.5.39)
которую мы будем называть магнитной.
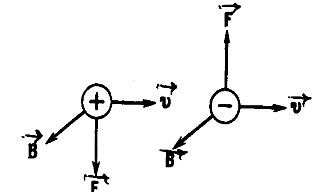
Направлена магнитная сила перпендикулярно к плоскости, в которой лежат векторы 
и 
. Если заряд положителен, направление силы совпадает с направлением вектора 
. В случае отрицательного заряда направления векторов 
и 
противоположны (рис. 3.5.9).
Магнитная сила всегда направлена перпендикулярно к скорости заряженной частицы, поэтому она работы над частицей не совершает. Следовательно, действуя на заряженную частицу постоянным магнитным полем, изменить её энергию нельзя.
Рис. 3.5.9 |
В случае, когда имеются одновременно электрическое и магнитное поля, сила, действующая на заряженную частицу, равна:
(3.5.40)
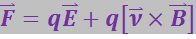
Это выражение было получено Лоренцем путём обобщения экспериментальных данных и носит название силы Лоренца.
к к к