ФИЗИКА

3.5.6. Закон Био-Савара-Лапласа

Био и Савар провели исследование магнитных полей, создаваемых токами, текущими по тонким проводам различной формы. Лаплас проанализировал экспериментальные данные и установил зависимость, которая получила название закона Био-Савара-Лапласа. Согласно этому закону магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками тока. Для магнитной индукции поля, создаваемого элементом тока длины , Лаплас получил формулу

(3.5.24)

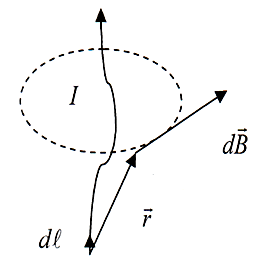
где – вектор, совпадающий с элементарным участком тока и направленный в ту сторону, в какую течёт ток (рис. 5.5);

– вектор, проведённый от элемента тока в ту точку, в которой определяется ;

r – модуль этого вектора;

– магнитная постоянная

(3.5.25)

где Гн (генри) – единица индуктивности.

Из рис. 5.5.5 видно, что вектор направлен перпендикулярно к плоскости, проходящей через и точку, в которой вычисляется поле, причём так, что вращение вокруг в направлении связано с правилом правого винта. Модуль определяется выражением

(3.5.26)

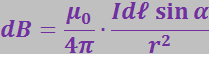
где α – угол между векторами и .

Применим формулу (3.5.26) для вычисления полей в трёх частных случаях.

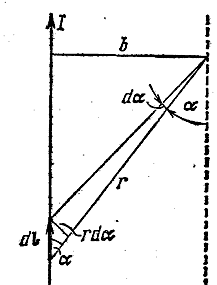
1. Поле тока, текущего по тонкому прямому проводу бесконечной длины (рис. 3.5.6). Все векторы в данной точке имеют одинаковое направление (в нашем случае за чертёж). Поэтому сложение векторов можно заменить сложением их модулей. Точка, для которой мы вычисляем магнитную индукцию, находится на расстоянии b от провода.

Из рисунка 3.5.6 видно, что

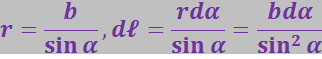
Подставим эти значения в формулу (3.5.26):

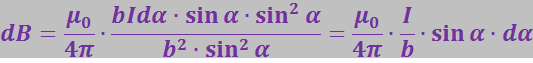
Угол α  для всех элементов бесконечного прямого тока изменяется в пределах от 0 до π. Следовательно,

(3.5.27)

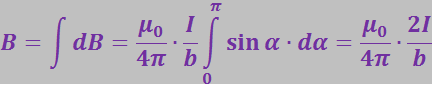
Линии магнитной индукции поля прямого тока представляют собой систему охватывающих провод концентрических окружностей.

2. Поле в центре кругового тока, т.е. тока, текущего по тонкому проводнику, имеющему форму окружности радиуса R. Каждый элемент тока создаёт в центре индукцию, направленную вдоль положительной нормали к контуру (рис. 3.5.7). Поэтому векторное сложение сводится к сложению их модулей. По формуле (3.5.26):

(3.5.28)

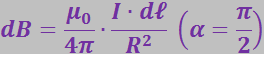
Интегрирование (3.5.28) даёт:

(5.29)

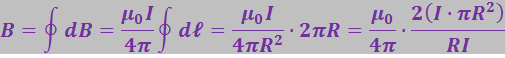
Величина в скобках называется модулем дипольного магнитного момента контура с током. Его направление совпадает с направлением положительной нормали к контуру:

(3.5.30)

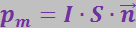
С учётом этого, формулу (3.5.29) можно представить в виде:

(3.5.31)

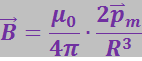
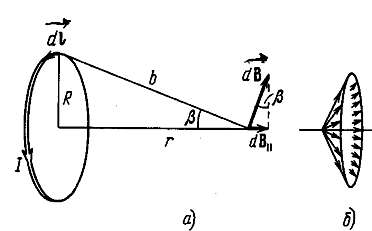
3. Поле на оси кругового тока. Возьмём точку на оси кругового тока на расстоянии r от центра контура (рис. 3.5.7). Векторы перпендикулярны к плоскостям, проходящим через соответствующий элемент тока и точку, в которой определяется поле.

Следовательно, они образуют симметрический конический веер (рис. 3.5.7б). Из соображений симметрии ясно, что результирующий вектор направлен вдоль оси контура. Каждый из векторов вносит результирующий вектор вклад , равный по модулю:

(3.5.32)

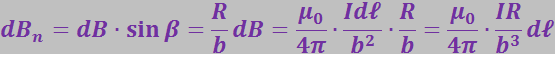
. Проинтегрировав по всему контуру и заменив b на , получим модуль вектора В:

(3.5.33)

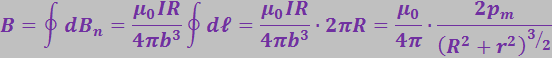
При r >> R можно пренебречь R2, тогда

(3.5.34)

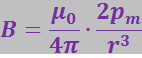
Поскольку и имеют одинаковое направление, формулу (3.5.33) можно написать в векторном виде:

(3.5.35)

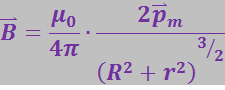
Эта формула определяет в точках оси по обе стороны от контура (справа и слева). Таким образом, в точках оси, симметричных относительно центра тока, магнитная индукция одинакова по модулю и направлению.

к к к