ФИЗИКА
3.5.4. Взаимодействие между движущимися зарядами
Пусть два точечных заряда Q и q расположены на расстоянии r друг от друга и неподвижны относительно системы xyz (рис. 3.5.3а). Между зарядами в этом случае действует кулоновская сила:
(3.5.12)
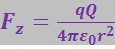
Рис. 3.5.3 |
Определим, какие силы действуют между этими же зарядами в системе отсчёта ![]() , которая движется вдоль оси абсцисс со скоростью
, которая движется вдоль оси абсцисс со скоростью ![]() (рис. 3.5.3б).
(рис. 3.5.3б).
Согласно (3.5.11):
(3.5.13)
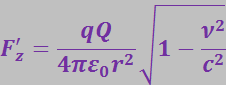
Относительно системы ![]() заряды Q и q движутся со скоростью
заряды Q и q движутся со скоростью ![]() параллельно друг другу. Оказывается, что сила взаимодействия между зарядами в этой системе отсчёта меньше, чем в системе xyz, относительно которой они покоятся. Умножив числитель и знаменатель выражения (3.5.13) на
параллельно друг другу. Оказывается, что сила взаимодействия между зарядами в этой системе отсчёта меньше, чем в системе xyz, относительно которой они покоятся. Умножив числитель и знаменатель выражения (3.5.13) на 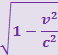 и разложив числитель на два слагаемых, получим:
и разложив числитель на два слагаемых, получим:
(3.5.14)
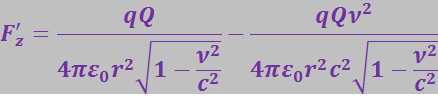
Первое слагаемое в этом выражении мы можем рассматривать как электрическую составляющую поперечной силы:
(3.5.15)

где Е – напряжённость поперечного электрического поля в системе отсчёта ![]() :
:
(3.5.16)
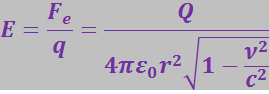
Второе слагаемое в (3.5.14) можно рассматривать как магнитную составляющую поперечной силы:
(3.5.17)
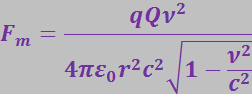
Разделив (3.5.17) на (3.5.15), получим отношение магнитной составляющей к электрической:
(5.18)
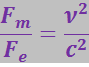
Отсюда, магнитная составляющая поперечной силы значительно меньше электрической. Поэтому при вычислении силы взаимодействия между свободными зарядами можно в первом приближении пренебречь магнитными силами и вести расчёт по известным формулам электростатики. Однако в случае, когда заряды движутся в проводнике, электрические силы оказываются скомпенсированными, и остаётся одна лишь магнитная сила. Именно этим и объясняется магнитное взаимодействие проводников с током, а также и другие случаи магнитных взаимодействий – в электромагнитах, электродвигателях и т.п.
к к к