ФИЗИКА

3.5.3. Закон преобразования для поперечного импульса и поперечной силы

Найдём преобразования для проекций импульса и силы вдоль аппликат, т.е. для поперечного импульса и поперечной силы. Пусть материальная точка с массой m0 движется со скоростью вдоль оси аппликат. Тогда проекция её импульса на эту ось:

(3.5.4)

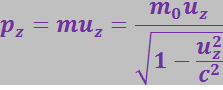
(Напомним, что согласно релятивистской динамики ).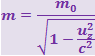

Проекция силы на эту же ось:

(3.5.5)

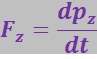
Определим составляющие импульса и силы в другой системе отсчёта, которая движется равномерно вдоль оси абсцисс со скоростью (рис. 3.5.2).

Поскольку рассматривается движение тела только вдоль оси аппликат, то абсцисса тела не меняется (x = const). Согласно преобразованиям Лоренца здесь:

(3.5.6)

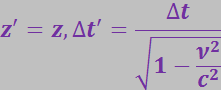
проекция скорости тела на ось аппликат в новой системе отсчёта:

(3.5.7)

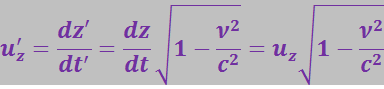
Масса в новой системе отсчёта:

(3.5.8)

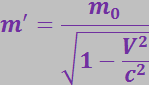
Отметим, что в формулах (3.5.6) и (3.5.7) фигурируют разные скорости. Дело в том, что часы мы считаем всегда покоящимися относительно системы отсчёта, поэтому в закон преобразования времени входит скорость движения одной системы отсчёта относительно другой v. Тело же движется относительно обеих систем отсчёта: относительно xyz – со скоростью , относительно – со скоростью (рис. 3.5.2). Именно эта скорость и входит в закон преобразования массы.

Имеем далее:

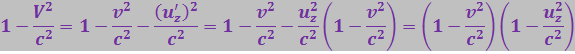
Подставив в (3.5.8), получим, учитывая (3.5.2):

(3.5.9)

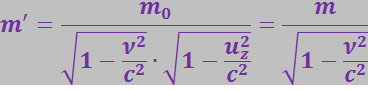
Найдём поперечный импульс в новой системе отсчёта. Используя (3.5.7) и (3.5.9), имеем:

(3.5.10)

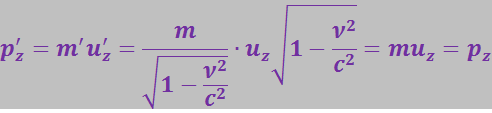
Итак, при переходе от одной инерциальной системы отсчёта к другой поперечный импульс не меняется.

Поперечная сила в новой системе отсчёта имеет вид:

(3.5.11)

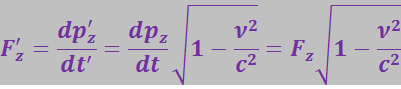
Итак, в отличие от ньютоновской механики, в теории относительности поперечная сила зависит от скорости, что и позволяет объяснить происхождение магнитных сил.

к к к