ФИЗИКА

3.5.2. Электрическое поле, измеренное в разных системах отсчёта

Многими опытами подтверждено, что заряд инвариантен относительно преобразования Лоренца. Тогда электрическое поле должно преобразовываться определённым образом. «Преобразовать поле » значит ответить на такой вопрос: если наблюдатель в некоторой инерциальной системе отсчёта К в данной точке пространства и времени измеряет поле и получает столько-то вольт на метр, то какое поле будет измерено в той же пространственно-временной точке наблюдателем в другой инерциальной системе отсчёта K' ? Ответим на этот вопрос, применяя теорему Гаусса к некоторой простой системе.

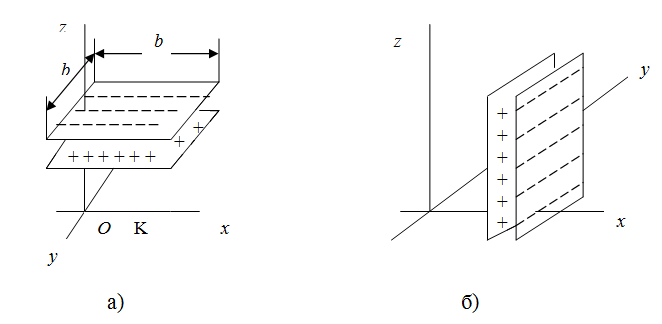
Рассмотрим в системе отсчёта К (рис. 3.5.1) два неподвижных и однородно заряженных слоя с поверхностной плотностью, равной, соответственно, +σ и -σ. Слои представляют собой квадраты со сторонами b, параллельные плоскости xy.

Предположим, что расстояние между слоями мало по сравнению с b, так что поле между ними можно считать однородным. Величина этого поля, измеренная наблюдателем в К, равна, конечно, (это следует из теоремы Гаусса). Теперь рассмотрим инерциальную систему K', движущуюся по отношению к К налево вдоль оси х (оси х и x' совпадают) со скоростью v. Для наблюдателя в K' заряженные «квадраты» уже больше не квадраты. Сторона x' сокращается от величины b до . Поэтому плотность заряда, измеренная в K', будет определяться соотношением:

(3.5.1)

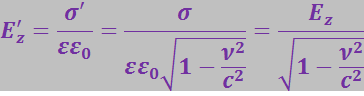
Теперь представим себе другую ситуацию, когда неподвижные в системе К слои ориентированы перпендикулярно к оси х, как показано на рис. 3.5.1б. Наблюдатель в К теперь сообщает нам, что поле в направление х имеет величину (теорема Гаусса). В этом случае поверхностная плотность заряда, наблюдаемая в системе K', такая же, как и наблюдаемая в системе К. Размеры слоёв не сокращаются; сокращается только расстояние между ними, но оно не входит в определение поля. С учётом этого

(3.5.2)

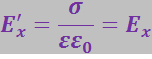
Всё это верно для рассмотренного здесь простейшего расположения зарядов; однако имеют ли наши выводы более общее значение? Этот вопрос приводит нас к самой сути понятия поля. Если понятие электрического поля в пространственно-временной точке должно иметь однозначный смысл, тогда значение поля в этой же пространственно-временной точке, но в других системах отсчёта не может зависеть от природы создающих поле источников, какими бы они ни были. Другими словами, наблюдатель в К, измеривший в некоторый момент времени поле около себя, должен быть в состоянии предсказать только на основании этих измерений, что измерят в той же пространственно-временной точке наблюдатели из других систем отсчёта. Если бы это было не так, поле было бы бесполезным понятием.

В общем случае соотношения (3.5.1) и (3.5.2) могут быть записаны так:

(3.5.3)

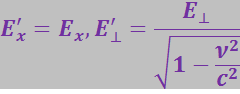
к к к