ФИЗИКА
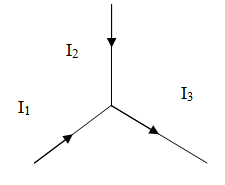
В основе расчёта разветвлённых электрических цепей лежат два правила Кирхгофа. Первое правило относится к узлам цепи. Узлами называются точки, в которых сходятся более чем два проводника (рис. 3.4.4). Току, текущему к узлу приписывается один знак (плюс или минус), току, текущему от узла – другой знак.
Рис. 3.4.4 |
Первое правило Кирхгофа гласит, что алгебраическая сумма токов, сходящихся в узле, равна нулю:
(3.4.27)
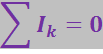
Это вытекает из следующих соображений. В цепи постоянного тока ничто не должно изменяться. В частности потенциалы во всех точках должны оставаться постоянными. Если бы алгебраическая сумма токов была отлична от нуля, то в узле происходило бы накапливание или уменьшение зарядов, что в свою очередь приводило бы к изменению потенциала узла. Уравнение (3.4.27) можно написать для всех N узлов. Однако независимыми будут только N - 1 уравнений, N-е будет следствием остальных.
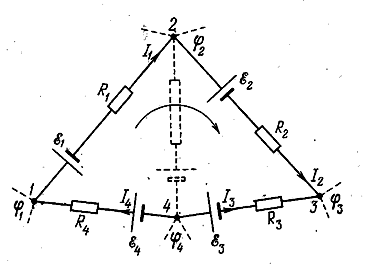
Второе правило относится к любому выделенному мысленно в разветвлённой цепи замкнутому контуру (рис. 3.4.5).
Рис. 3.4.5 |
Выберем направление обхода (например, по часовой стрелке, как показано на рисунке) и применим к каждому из участков контура закон Ома:
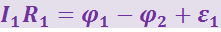
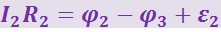


Если сложить эти равенства, потенциалы сократятся, и получится уравнение:
(3.4.28)
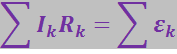
которое выражает второе правило Кирхгофа.
Уравнение (3.4.28) можно составить для всех замкнутых контуров, которые можно выделить в данной цепи. Однако независимыми будут только уравнения для тех контуров, которые нельзя получить наложением для них других контуров. Например, контур 1-2-3-4-1 на рис. 3.4.5 получается наложением контуров 1-2-4-1 и 2-3-4-2. Поэтому независимыми будут уравнения для любых двух контуров из этих трёх.
При составлении уравнений направления токов и направление обхода можно выбирать произвольно. Токам и э.д.с. нужно приписывать знаки в соответствии с направлением обхода. Например, ток I3 на рис. 3.4.5 нужно считать отрицательным, так как он изображён текущим навстречу направлению обхода. Э.д.с. ε1 и ε2 также нужно считать отрицательными, поскольку они действуют в направлении, противоположном указанному на рисунке.
Надо иметь в виду, что через любое сечение неразветвлённого участка цепи течёт один и тот же ток. Например, на участке от точки 1 до источника тока ε1 течёт такой же ток I1, как и на участке от источника тока ε1 до точки 2.
Число независимых уравнений, составленных по первому и второму правилам Кирхгофа, равно количеству токов, текущих в разных звеньях цепи. Поэтому если заданы э.д.с. и сопротивления, то могут быть вычислены все токи. Можно решить и задачи иного рода, например, найти э.д.с. (или сопротивления), которые нужно включить в каждое звено цепи, чтобы получить при заданных сопротивлениях (или э.д.с.) нужные токи.
к к к