ФИЗИКА
Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному (в смысле отсутствия сторонних сил) металлическому проводнику, пропорциональна падению напряжения на проводнике:
(3.4.15)
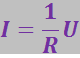
где R – электрическое сопротивление проводника.
Единицей сопротивления служит ом (Ом), равный сопротивлению такого проводника, в котором при напряжении в 1 В течёт ток силы 1 А.
Электрическое сопротивление зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан. Для однородного цилиндрического проводника:
(3.4.16)
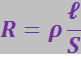
где ℓ – длина проводника;
S – площадь его поперечного сечения;
ρ – зависящий от материала коэффициент, называемый удельным электрическим сопротивлением вещества.
Если ℓ = 1 м и S = 1, то R численно равно ρ. Измеряется ρ в ом-метрах (Ом ⋅м).
Найдём связь между векторами ![]() и
и ![]() в одной и той же точке проводника. В изотропном проводнике упорядоченное движение носителей тока происходит в направлении вектора
в одной и той же точке проводника. В изотропном проводнике упорядоченное движение носителей тока происходит в направлении вектора ![]() . Поэтому направления векторов
. Поэтому направления векторов ![]() и
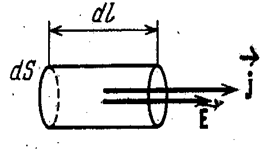
и ![]() совпадают. Выделим мысленно в окрестности некоторой точки элементарный цилиндрический объём с образующими, параллельными векторами
совпадают. Выделим мысленно в окрестности некоторой точки элементарный цилиндрический объём с образующими, параллельными векторами ![]() и
и ![]() (рис. 3.4.2).
(рис. 3.4.2).
Рис. 3.4.2 |
Через поперечное сечение цилиндра течёт ток силой jdS. Напряжение, приложенное к цилиндру, равно ![]() , где Е – напряжённость поля в данном месте. Сопротивление цилиндра равно
, где Е – напряжённость поля в данном месте. Сопротивление цилиндра равно ![]() . Подставив эти значения в формулу (3.4.15), получим:
. Подставив эти значения в формулу (3.4.15), получим:
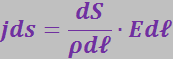
или
 ,
,
или в векторной форме:
(3.4.17)
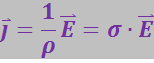
Эта формула выражает закон Ома в дифференциальной форме.
Выражение ![]() называется удельной электрической проводимостью. Единица, обратная ому, называется сименсом (См). Соответственно единицей ρ является сименс на метр (См / м).
называется удельной электрической проводимостью. Единица, обратная ому, называется сименсом (См). Соответственно единицей ρ является сименс на метр (См / м).
Допустим для простоты, что в проводнике имеются носители лишь одного знака. Тогда согласно (3.4.5) плотность тока равна:
(3.4.18)
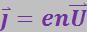
Сравнение этого выражения с формулой (3.4.18) приводит к выводу, что скорость упорядоченного движения носителей тока пропорциональна напряжённости поля ![]() , т.е. силе, сообщающей носителям упорядоченное движение. Пропорциональность скорости приложенной к телу силе наблюдается в тех случаях, когда кроме силы, вызывающей движение, на тело действует сила сопротивления среды. Эта сила вызывается взаимодействием носителей тока с частицами, из которых построено вещество проводника. Наличие силы сопротивления упорядоченному движению носителей тока обусловливает электрическое сопротивление проводника.
, т.е. силе, сообщающей носителям упорядоченное движение. Пропорциональность скорости приложенной к телу силе наблюдается в тех случаях, когда кроме силы, вызывающей движение, на тело действует сила сопротивления среды. Эта сила вызывается взаимодействием носителей тока с частицами, из которых построено вещество проводника. Наличие силы сопротивления упорядоченному движению носителей тока обусловливает электрическое сопротивление проводника.
Величина ρ или σ определяется химической природой вещества и условиями, в частности температурой, при которых оно находится.
Для большинства металлов при температурах, близких к комнатной, ρ изменяется пропорционально абсолютной температуре:
(3.4.19)

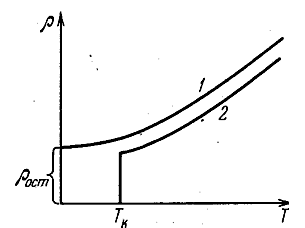
При низких температурах наблюдаются отступления от этой закономерности (рис. 3.4.3).
Рис. 3.4.3 |
В большинстве случаев зависимость ρ от Т следует кривой 1. Величина остаточного сопротивления ![]() в сильной степени зависит от частоты материала и наличия остаточных механических напряжений в образце. Поэтому после отжига
в сильной степени зависит от частоты материала и наличия остаточных механических напряжений в образце. Поэтому после отжига ![]() заметно уменьшается. У абсолютно чистого металла с идеальной кристаллической решёткой при абсолютном нуле
заметно уменьшается. У абсолютно чистого металла с идеальной кристаллической решёткой при абсолютном нуле ![]() .
.
У большой группы металлов и сплавов, а также керамических материалов при достаточно низкой температуре сопротивление скачком обращается в нуль (кривая 2). Впервые это явление, названное сверхпроводимостью, было обнаружено в 1911 г. Камерлинг-Оннесом.
Для каждого сверхпроводника имеется своя критическая температура TK, при которой он переходит в сверхпроводящее состояние. У металлов и сплавов эта температура составляет несколько кельвин, у керамических материалов – несколько десятков кельвин.
Сопоставление формул (3.4.6) и (4.17) приводит к выводу, что скорость упорядоченного движения носителей тока пропорциональна напряжённости поля:
(3.4.20)

Величины ![]() и
и ![]() называются подвижностью соответствующего носителя тока. Подвижность численно равна скорости упорядоченного движения носителя тока при напряжённости поля, равной единице.
называются подвижностью соответствующего носителя тока. Подвижность численно равна скорости упорядоченного движения носителя тока при напряжённости поля, равной единице.
Подстановка соотношений (3.4.20) в формулу (3.4.6) даёт
(3.4.21)

откуда
(3.4.22)
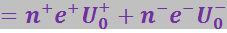
На неоднородном участке цепи средняя скорость упорядоченного движения носителей тока пропорциональна сумме напряжённости электростатического поля и напряжённости поля сторонних сил. Соответственно плотность тока:
(3.4.23)
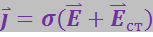
Эта формула обобщает формулу (3.4.17) на случай неоднородного проводника.
Рассмотрим цилиндрический проводник с площадью поперечного сечения S и длиной ℓ. Допустим, что напряжённости ![]() и
и ![]() во всех точках проводника одни и те же. Умножим обе части равенства (3.4.23) на перемещение
во всех точках проводника одни и те же. Умножим обе части равенства (3.4.23) на перемещение ![]() вдоль оси проводника и проинтегрируем получившееся соотношение по длине проводника от 0 до ℓ . В результате получим:
вдоль оси проводника и проинтегрируем получившееся соотношение по длине проводника от 0 до ℓ . В результате получим:
(3.4.24)
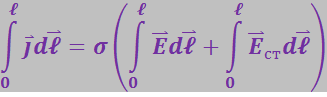
Интеграл, стоящий слева, равен ![]() . Интегралы справа равны соответственно разности потенциалов
. Интегралы справа равны соответственно разности потенциалов ![]() между концами проводника и э.д.с. ε12, действующей в проводнике. Учтя это и заменив
между концами проводника и э.д.с. ε12, действующей в проводнике. Учтя это и заменив ![]() и
и ![]() , можно написать (3.4.24) в виде:
, можно написать (3.4.24) в виде:
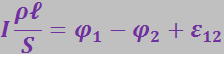
или с учётом (3.4.16):
(3.4.25)
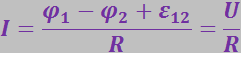
Формула (3.4.25) выражает закон Ома для неоднородного участка цепи. В ней сила тока и э.д.с. – величины алгебраические. Сила тока положительна, когда ток течёт в направлении от конца проводника 1 к концу 2. Э.д.с. считается положительной, если она способствует движению положительных носителей в направлении 1-2.
Для замкнутой цепи ![]() . Тогда
. Тогда
(3.4.26)
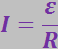
где ε – э.д.с., действующая в цепи;
R – суммарное сопротивление всей цепи.
к к к