ФИЗИКА
Молекулой называется наименьшая частица однородного вещества, обладающая его основными химическими свойствами. Молекулы состоят из одинаковых или различных атомов, соединённых между собой межатомными химическими связями.
Чтобы понять причины, по которым электрически нейтральные атомы могут образовать устойчивую молекулу, ограничимся рассмотрением простейших двухатомных молекул, состоящих из двух одинаковых или различных атомов. Силы межатомного взаимодействия возникают между внешними валентными электронами атомов. Об этом говорит резкое изменение оптического спектра атомов при вступлении их в химические соединения. Наоборот, рентгеновские характеристические спектры, зависящие от внутренних, глубинных электронов атомов, при вступлении атомов в химические соединения не изменяются.
Какой бы ни была природа тех сил, которые объединяют атомы в молекулу, можно высказать некоторые общие соображения о характере этих сил. Если атомы находятся на большом расстоянии друг от друга, то они не взаимодействуют между собой. При сближении атомов возрастают силы взаимного притяжения. На малых расстояниях, сравнимых (и меньших) с линейными размерами атомов, проявляют себя силы взаимного отталкивания, которые не позволяют электронам одного атома слишком глубоко проникать внутрь электронных оболочек другого атома.
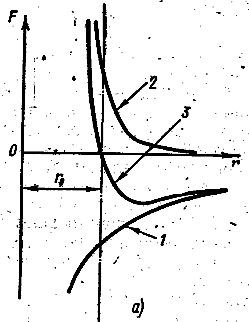
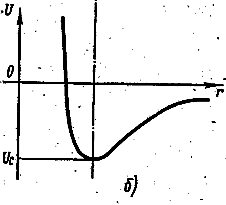
Силы притяжения и отталкивания по-разному зависят от расстояния r между атомами. Силы отталкивания быстрее изменяются при изменении r, являются более «короткодействующими», чем силы притяжения. При увеличении расстояния r между атомами силы отталкивания убывают быстрее, чем силы притяжения. Одновременное действие противоположно направленных сил – притяжения и отталкивания – приводит к тому, что на некотором расстоянии r0 между атомами обе силы уравновешивают друг друга и их геометрическая сумма становится равной нулю. Этому расстоянию соответствует наименьшая потенциальная энергия U(r) двухатомной молекулы. На рис. 6.7.1а приведены три кривые: сила притяжения (кривая 1), сила отталкивания (кривая 2) и результирующая сила взаимодействия (кривая 3) атомов в двухатомной молекуле в зависимости от расстояния r между атомами. Силы отталкивания считаются положительными. На рис. 6.7.1б приведена кривая зависимости от r потенциальной энергии U взаимодействия атомов в двухатомной молекуле.
Рис. 6.7.1 |
Равновесное межатомное расстояние r0 в молекуле называется длиной связи. Величина Uc называется энергией диссоциации молекулы, или энергией связи. Она численно равна работе, которую надо совершать для того, чтобы разорвать химические связи атомов в молекуле и удалить атомы друг от друга за пределы действия междуатомных сил.
Наиболее часто в молекулах встречаются два типа связи: ионная и ковалентная.
Ионная связь (например, в молекулах NaCl, KBr) осуществляется электростатическим взаимодействием атомов при переходе электрона одного атома к другому, т.е. при образовании положительного и отрицательного ионов.
Ковалентная связь (например, в молекулах H2, C2, CO) осуществляется при обобществлении валентных электронов двумя соседними атомами (спины валентных электронов должны быть антипараллельны). Ковалентная связь объясняется на основе принципа неразличимости тождественных частиц, например, электронов в молекуле водорода. Неразличимость частиц приводит к специфическому взаимодействию между ними, называемому обменным взаимодействием. Это чисто квантовый эффект, не имеющий классического объяснения, но его можно представить себе так, что электрон каждого из атомов молекулы водорода проводит некоторое время у ядра другого атома. При этом оба электрона большую часть времени проводят в пространстве между ядрами. В результате их отрицательный заряд стягивает ядра, образуя молекулу водорода.
Молекула является квантовой системой; она описывается уравнением Шредингера, учитывающим движение электронов в молекуле, колебания атомов молекулы, вращение молекулы.
Соответственно энергия изолированной молекулы может быть представлена суммой
(6.7.1)
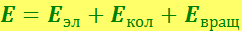 ,
,
где Eэл - энергия движения электронов относительно ядер;
Екол - энергия колебания ядер;
Евращ - энергия вращения ядер.
Из теории и эксперимента Еэл ≈ 1 ÷ 10 эВ, Екол ≈ 10–2 ÷ 10–1 эВ, Евращ ≈ 10–5 ÷ 10–3 эВ. Отсюда Еэл >> Екол >> Евращ.
Каждая из входящих в выражение (6.7.1) энергий квантуется и определяется квантовыми числами. При переходе из одного энергетического состояния в другое поглощается или испускается энергия ΔЕ = hν. При таких переходах одновременно изменяются энергия движения электронов, энергия колебаний и вращения. Из теории и эксперимента следует, что расстояния между вращательными уровнями энергии ΔЕвращ гораздо меньше расстояний между колебательными уровнями энергии ΔЕкол, которые, в свою очередь, меньше расстояний между электронными уровнями ΔЕэл.
Структура энергетических уровней молекул определяет их спектры.
Молекулярные спектры при наблюдении в прибор средней разрешающей силы представляются состоящими из полос. В соответствии с этим спектры молекул носят название полосатых. В зависимости от того, изменение каких видов энергии (электронной, колебательной или вращательной) обусловливает испускание молекулой фотона, различают три вида полос:
1) вращательные;
2) колебательно-вращательные
3) электронно-колебательные.
Мы ограничимся рассмотрением вращательных и колебательно-вращательных спектров двухатомных молекул.
Начнём с вращательных спектров. Энергия молекулы, имеющей момент инерции J и вращающейся с угловой скоростью ω, равна
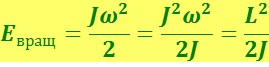 ,
,
где L = Jω - момент импульса молекулы.
Как известно, момент импульса может принимать лишь дискретные значения:
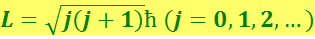
(j – квантовое число момента импульса).
Следовательно, вращательная энергия молекулы может иметь только квантованные значения:
(6.7.2)
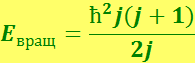
где J – момент инерции молекулы относительно оси, проходящей через её центр инерции;
j – вращательное квантовое число, принимающее значения 0, 1, 2 и т.д.
Для вращательного квантового числа имеется правило отбора
(6.7.3)
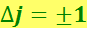
Поэтому частоты линий, испускаемых при переходах между вращательными уровнями могут иметь значения:
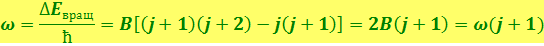 ,
,
где j – квантовое число уровня, на который совершается переход (оно может иметь значения: 0, 1, 2,…), а
(6.7.4)

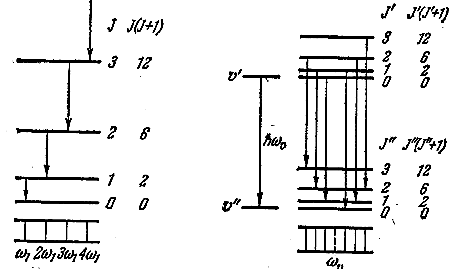
На рис 6.7.2 а показана схема возникновения вращательной полосы. Вращательный спектр состоит из ряда равноотстоящих линий, расположенных в очень далёкой инфракрасной области. Измерив расстояние между линиями Δω = ω1, можно определить константу (6.7.4) и найти момент инерции молекулы. Затем, зная массы ядер, можно вычислить равновесное расстояние между ними R0 в двухатомной молекуле. Например, для молекулы HCl J = 2,71 ⋅ 10-40 г ⋅ см2 , что соответствует R0 = 1,29E.
а) б) Рис. 6.7.2 |
Теперь рассмотрим колебательно-вращательные полосы. Можно полагать, что ядра колеблются как квантовый гармонический осциллятор. Его энергия определяется выражением
(6.7.5)
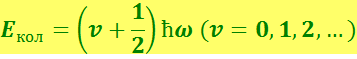
где υ - колебательное квантовое число;
ω - классическая частота осциллятора.
Для колебательного квантового числа имеется правило отбора
(6.7.6)
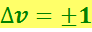
Кривая потенциальной энергии молекулы (рис. 6.7.1б) совпадает с параболой только при малых колебаниях. Ангармоничность (отклонения от гармоничности), наступающая при увеличении интенсивности колебаний, приводит к тому, что с увеличением квантового числа υ уровни сгущаются, имея своим пределом энергию E0 диссоциированной молекулы. Однако при небольших значениях υ можно с достаточной степенью точности считать, что колебательная энергия молекулы определяется формулой (6.7.5).
При излучении фотонов колебательно-вращательной полосы изменяются также колебательная и вращательная энергии молекулы. С учётом этого энергия излучаемого фотона будет равна
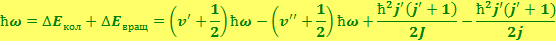
Поскольку ΔЕкол >> ΔЕвращ, испускание фотона может наблюдаться не только при j' > j", но и при j' < j". В случае j' > j" частоты фотонов определяются формулой
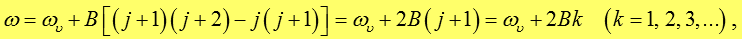
где j - вращательное квантовое число нижнего уровня, которое может принимать значения: 0, 1, 2,…; ![]() .
.
Если j' < j", формула для частоты фотонов имеет вид
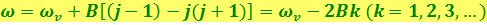 ,
,
где j – вращательное квантовое число нижнего уровня.
Оба случая можно описать одной формулой:
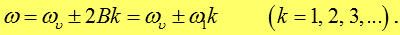
Совокупность линий с частотами, определяемыми этой формулой, называется колебательно-вращательной полосой. Область, в которой располагаются колебательно-вращательные полосы, простирается от 8000 до 50000 Å.
В полном соответствии с теорией вращательные и колебательно-вращательные спектры наблюдаются только для несимметричных двухатомных молекул.
Комбинационное рассеяние света. В 1928 г. группой учёных было открыто явление, заключающееся в том, что в спектре рассеяния, возникающем при прохождении света через газы, жидкости или прозрачные кристаллические тела, помимо несмещённой линии, содержатся новые линии, частоты которых ω представляют собой комбинацию частоты падающего света ω0 и частот ωi колебательных или вращательных переходов рассеивающих молекул:
(6.7.7)

Это явление получило название комбинационного рассеяния света, а новые линии стали называть спутниками. Каждому «красному» спутнику (т.е. спутнику, смещённому в сторону больших длин волн) с частотой ω0 - ωi соответствует «фиолетовый» спутник с частотой ω0 + ωi. При обычных температурах интенсивность фиолетовых спутников значительно меньше, чем красных. С повышением температуры интенсивность фиолетовых спутников быстро растёт.
Это явление легко объясняется в квантовой теории. Согласно её представлениям процесс рассеяния света можно рассматривать как неупругое соударение фотонов с молекулами. При соударении фотон может отдать молекуле или получить от неё только такие количества энергии, которые равны разностям двух её энергетических уровней. Если при столкновении с фотоном молекула переходит в состояние с большей энергией, то энергия фотона после рассеяния станет равной ħω0 = ΔE, где ΔE - энергия, переданная фотоном молекуле. Соответственно частота фотона уменьшится и возникнет красный спутник. Если перед столкновением с фотоном молекула находилась в возбуждённом состоянии (с бóльшей энергией), то она может при столкновении с фотоном перейти в состояние с меньшей энергией, отдав избыток энергии ΔE фотону. В результате энергия фотона станет равной ħω0 + ΔE и возникает фиолетовый спутник.
Рассеяние фотона ħω0 может сопровождаться переходами молекулы между различными вращательными или колебательными уровнями. В итоге возникает ряд симметрично расположенных спутников.
При обычных температурах число молекул, находящихся в основном состоянии, намного превосходит число молекул, находящихся в возбуждённых состояниях. Поэтому столкновения, сопровождающиеся уменьшением энергии молекулы, происходят гораздо реже, чем переходы, сопровождающиеся увеличением энергии. Этим объясняется малая интенсивность фиолетовых спутников по сравнению с красными. При повышении температуры число возбуждённых молекул быстро растёт, что приводит к увеличению интенсивности фиолетовых спутников.
Исследование комбинационного рассеяния даёт много сведений о строении молекул. С помощью этого метода определяются собственные частоты колебаний молекулы; он позволяет также судить о характере симметрии молекулы. Спектры комбинационного рассеяния настолько характерны для молекул, что с их помощью осуществляют анализ сложных молекулярных смесей, особенно органических молекул, анализ которых химическими методами весьма затруднён или даже невозможен.
к к к