ФИЗИКА

6.3.7. Атом водорода в квантовой механике. Спин электрона

Рассмотрим систему, состоящую из неподвижного ядра с зарядом Ze.

(Z – целое число) и движущегося вокруг него электрона. При Z>1 такая система называется водородоподобным ионом; при Z = 1 она представляет собой атом водорода.

Потенциальная энергия электрона равна

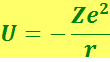
(r – расстояние электрона от ядра).

Следовательно, уравнение Шредингера имеет вид

(6.5.6)

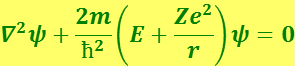
где m – масса электрона.

Можно показать, что уравнение (6.5.6) имеет требуемые (т.е. однозначные, конечные и непрерывные) решения в двух случаях:

1) при любых положительных энергиях Е;

2) при дискретных отрицательных значениях энергии, равных

(6.5.7)

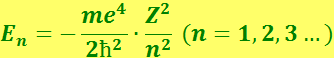
Случай Е > 0 соответствует электрону, пролетающему вблизи ядра и удаляющемуся снова на бесконечность. Случай Е < 0 соответствует электрону, связанному с ядром. Такой же результат для энергии водородного атома получается и в теории Бора. Однако в квантовой механике этот результат получается как следствие основных положений этой теории.

Собственные функции уравнения (6.5.7) содержат три целочисленных параметра: n, ℓ и т:

(6.5.8)

Параметр n, называемый главным квантовым числом, совпадает с номером уровня энергии. Параметры ℓ и т представляют собой азимутальное и магнитное квантовые числа, определяющие по формулам

(6.5.9)

;

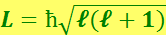(6.5.10)

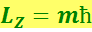
модуль момента импульса и проекцию момента импульса на некоторое направление Z.

Решения, удовлетворяющие стандартным условиям получаются лишь для значений ℓ, не превышающих n - 1.

Следовательно, при данном n квантовое число ℓ может принимать n различных значений:

.

При данном ℓ квантовое число т может принимать 2ℓ +1 различных значений:

.

Согласно (6.5.7), энергия электрона зависит только от главного квантового числа n. Следовательно, каждому собственному значению энергии (кроме Е1) соответствует несколько собственных функций ψn,e,m, отличающихся значениями квантовых чисел ℓ и т. Это означает, что атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях.

Состояния с одинаковой энергией называются вырожденными, а число различных состояний с каким-либо значением энергии называется кратностью вырождения соответствующего энергетического уровня.

Нетрудно показать, что кратность вырождения энергетических уровней атома водорода равна π2.

Принято электрон, находящийся в состоянии с ℓ = 0, называть s-электроном (а соответствующее состояние – s-состоянием), с ℓ = 1 – р-электроном, с ℓ = 2 – d-электроном, с ℓ = 3 – f-электроном, затем идут g, h и так далее уже по алфавиту. Значение главного квантового числа указывают перед условным обозначением квантового числа ℓ. Таким образом, электрон в состоянии с n = 4 и ℓ = 2 обозначают символом 4d и так далее.

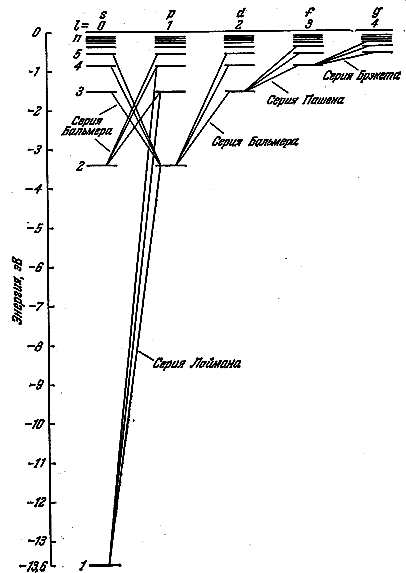
Одна из возможных схем уровней атома водорода показана на рис. 6.7.1. Как известно, испускание и поглощение света происходит при переходах электрона с одного уровня на другой. Для азимутального квантового числа ℓ имеется правило отбора

(6.5.11)

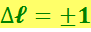
Это правило обусловлено тем, что фотон обладает собственным моментом импульса (спином), равным ħ. При испускании фотон уносит из атома этот момент, а при поглощении привносит, так что правило (6.7.6) есть просто следствие закона сохранения момента импульса.

На рис. 6.5.1 показаны переходы, разрешённые правилом (6.5.11). Пользуясь условными обозначениями состояний электрона, переходы, приводящие к возникновению серии Лаймана, можно записать в виде

.

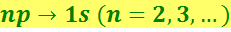Серии Бальмера соответствуют переходы

.

Серии Брэкета и Пашены показаны на рис. 6.5.1.

Состояние 1s является основным состоянием атома водорода. В этом состоянии атом обладает минимальной энергией. Чтобы перевести атом из основного состояния в возбуждённое (т.е. в состояние с большей энергией), ему необходимо сообщить энергию. Это может быть осуществлено за счёт теплового соударения атомов, или за счёт столкновения атома с достаточно быстрым электроном, или за счёт поглощения атомом фотона.

Фотон при поглощении его атомом исчезает, передавая атому всю свою энергию. Атом не может поглотить только часть фотона, ибо фотон, как и электрон, как и другие элементарные частицы, является неделимым. Поэтому в отсутствие многофотонных процессов атом может поглощать только те фотоны, энергия которых соответствует разности энергий двух его уровней. Поскольку поглощающий атом обычно находится в основном состоянии, спектр поглощения водородного атома должен состоять из линий, соответствующих переходам

.

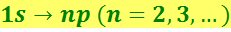Этот результат подтверждается опытом.

По мере роста главного квантового числа n уровни энергии (рис. 6.5.1) становятся всё гуще и гуще. Следовательно, присущая квантовой механике дискретность уровней уменьшается, и характер поведения частицы приближается к классическому. В этом проявляется установленный Бором принцип соответствия, согласно которому, в пределе при больших квантовых числах следствия, вытекающие из квантовой механики, должны совпадать с результатами классической теории.

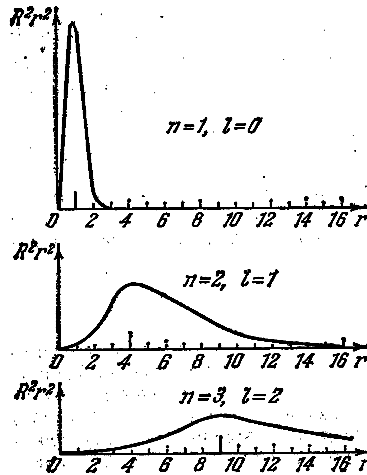
На рис. 6.5.2 приведены графики плотности вероятности для атома водорода в состояниях:

1) n = 1, ℓ = 0;

2) n = 2, ℓ = 1;

3) n = 3, ℓ = 2.

Длинными вертикальными чёрточками отмечены на графиках радиусы соответствующих боровских орбит. Из рисунка видно, что эти радиусы совпадают с наиболее вероятными расстояниями электрона от ядра. Из рисунка же следует, что электрон не находится на каком-то точно определённом расстоянии от ядра. Не существует и электронных «орбит»; вместо этого имеется «размытое» электронное распределение, и можно указать лишь вероятность того, что электрон находится на данном расстоянии от ядра.

Спин электрона. В 1921 г. О. Штерном и В. Герлахом были поставлены опыты, цель которых состояла в измерении магнитных моментов атомов различных химических элементов, в том числе атомов первой группы.

Особенность атомов первой группы состоит в том, что у них орбитальные механические (и магнитные) моменты всех электронов, кроме валентного, взаимно компенсируют друг друга, а значит, магнитный момент атома равен магнитному моменту одного электрона.

Идея опытов Штерна и Герлаха заключалась в измерении силы, действующей на атом в неоднородном магнитном поле. В этом поле на атом действует сила

(6.5.12)

,

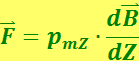где - индукция магнитного поля, направленного вдоль оси Z.

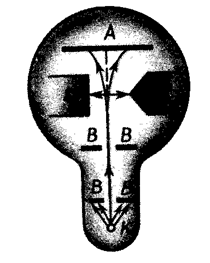
Результаты опытов обнаружили ошибочность классического предположения о том, что магнитный момент и механический момент импульса атома произвольно ориентируются относительно направления внешнего поля, и подтвердили наличие пространственного квантования. Схема первых опытов Штерна и Герлаха изображена на рис. 6.5.3.

В трубке, где был создан вакуум порядка 10-5 мм рт. ст., помещался источник пучка атомов – нагреваемый до высокой температуры серебряный шарик К. Атомы серебра вылетали с его поверхности со средней тепловой скоростью порядка 100 м/с, соответствующей температуре испарения серебра. Из этих атомов при помощи щелевых диафрагм Д вырезался узкий пучок, проходящий через сильное неоднородное магнитное поле, направленное перпендикулярно пучку. Основная трудность опыта состояла в том, чтобы достигнуть такой большой неоднородности магнитного поля, которая сказывалась бы на расстояниях порядка размеров атома. Необходимая неоднородность поля была получена в результате применения электромагнита SN с полюсными наконечниками специальной формы. Приёмником атомов серебра была фотопластинка А.

Если бы момент импульса атома (и его магнитный момент ) мог принимать произвольные ориентации в магнитном поле, то можно было бы ожидать непрерывного распределения попаданий атомов на пластинку с большей плотностью попаданий в середине пластинки и меньшей плотностью к её краям. Опыты, проведённые с серебром и атомами других элементов периодической системы, привели к совершенно другим результатам.

На рис. 6.5.4 показана фотография результата опыта с литием. Атомы в атомном пучке находились в основном состоянии. Из рисунка видно, что на фотопластинке получились две резкие полосы – все атомы отклонялись в магнитном поле двояко, что соответствовало лишь двум возможным ориентациям магнитного момента атома во внешнем поле. Напомним, что у лития моменты импульса и магнитные моменты атомов совпадают с моментами валентного электрона.

Если подставить

(6.5.13)

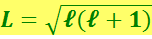
(6.5.14)

в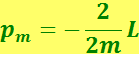  

то связь величин pm и ℓ можно записать в виде

(6.5.15)

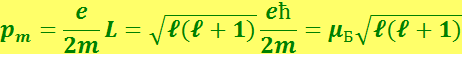
где - магнетон Бора (единица измерения магнитных моментов в атомной физике).

Важной особенностью атомов первой группы, а, значит, и лития, является то, что валентный электрон в основном состоянии атома находится в s-состоянии, а в s-состоянии ℓ = 0. Следовательно, согласно (6.5.13), равен нулю момент импульса электрона и связанный с ним (6.7.9) магнитный момент. В связи с этим возникает серьёзный вопрос: пространственное квантование какого момента импульса обнаружилось в этих опытах и проекция какого магнитного момента равна одному магнетону Бора?

Наряду с данной трудностью в то время существовали и другие. Так, в опытах Эйнштейна и де Гааза обнаружилось аномальное значение гиромагнитного отношения для ферромагнетиков. Кроме того, исследование спектров щелочных металлов при помощи приборов с большой разрешающей силой показало, что каждая линия этих спектров является двойной (дублет). Например, характерная для натрия жёлтая линия 3p → 3s состоит из двух линий с длинами волн 5890 и 5896 E.

Структура спектра, отражающая расщепление линий на компоненты, называется тонкой структурой. Сложные линии, состоящие из нескольких компонент, получили название мультиплетов. Тонкая структура обнаруживается, кроме щелочных металлов, также и у других элементов.

Расщепление спектральных линий, очевидно, обусловлено расщеплением энергетических уровней. Для объяснения расщепления уровней и вышеуказанных трудностей Гаудсмит и Уленбек выдвинули в 1925 г. гипотезу о том, что электрон обладает собственным моментом импульса Ls, не связанным с движением электрона в пространстве. Этот собственный момент был назван спином.

Первоначально предполагалось, что спин обусловлен вращением электрона – заряженного шарика – вокруг своей оси. Согласно этим представлениям, электрон уподоблялся волчку или веретену. Отсюда происходит и сам термин: по-английски spin означает «верчение». Однако скоро от подобных модельных представлений пришлось отказаться по следующей причине. Как показал расчёт, чтобы иметь тот спиновый магнитный момент, который электрон обнаруживает в опытах, ему необходимо вращаться со скоростью примерно в 200 раз большей, чем скорость света, а это противоречит теории относительности.

Таким образом, представление об электроне как о вращающемся шарике оказалось несостоятельным. Спин следует считать внутренним свойством, присущим электрону, подобно тому как ему присущи заряд и масса.

Предположение о спине электрона было подтверждено большим количеством опытных фактов и должно считаться совершенно доказанным. Оказалось также, что наличие спина и все его свойства автоматически вытекают из установленного Дираком уравнения квантовой механики, удовлетворяющего требованиям теории относительности. Таким образом, выяснилось, что спин электрона является свойством одновременно квантовым и релятивистским. Спином обладают также протоны, нейтроны, фотоны и другие элементарные частицы (кроме мезонов).

Величина собственного момента импульса электрона определяется так называемым спиновым квантовым числом s, равным 1/2:

(6.5.16)

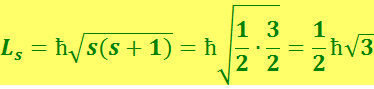
Проекция спина на заданное направление может принимать квантованные значения, отличающиеся друг от друга на ħ:

(6.5.17)

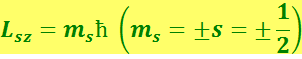
Чтобы найти значение собственного магнитного момента электрона ps, умножим Ls на отношение :

(6.5.18)

Знак минус указывает на то, что механический Ls и магнитный ps моменты электрона направлены в противоположные стороны.

Проекция собственного магнитного момента электрона на заданное направление может иметь следующие значения:

(6.5.19)

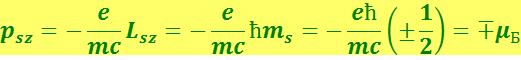
(минус получается, если , плюс – если ).

Таким образом, проекция собственного момента импульса электрона может принимать значения и , а собственного магнитного момента – значения +μ и -μ.

Принято говорить, что собственный механический момент (спин) электрона равен половине (подразумевается: в единицах ħ), а собственный магнитный момент равен одному магнетону Бора.

Рассмотрим теперь на примере атома натрия, как существование спина электрона может объяснить мультиплетную структуру спектра. Напомним: момент атома натрия равен моменту валентного электрона. Момент же электрона будет слагаться из двух моментов: орбитального L, обусловленного движением электрона в атоме, и спинового Ls, не связанного с движением электрона в пространстве. Результирующая этих двух моментов даёт полный момент импульса валентного электрона. Сложение орбитального и спинового моментов осуществляется по правилам квантовой механики. Величина полного момента αj определяется квантовым числом j:

,

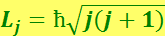j может иметь значения

,

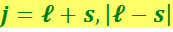где ℓ и s соответственно азимутальное и спиновое квантовые числа.

При ℓ = 0 j имеет одно значение . При ℓ, отличном от нуля, возможны два значения: и , которые соответствуют двум возможным взаимным ориентациям моментов L и Ls. Теперь учтём, что с механическими моментами связаны магнитные моменты, которые взаимодействуют друг с другом подобно тому, как взаимодействуют два тока или две магнитные стрелки. Энергия этого спинорбитального взаимодействия зависит от взаимной ориентации орбитального и спинового моментов. Следовательно, состояния с различным j должны обладать различной энергией.

Таким образом, каждый терм (терм – это числа, разность которых определяет частоту линии спектра) ряда p(ℓ = 1) расщепляется на два, соответствующих и ; каждый терм ряда D(ℓ = 2) расщепляется на термы с и и т.д.

Итак, каждый ряд термов, кроме S, распадается на два ряда – структура термов оказывается дублетной (двойной). Термы принято обозначать символами:

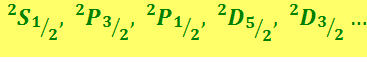
Правый нижний индекс даёт значение j. Верхний левый индекс указывает мультиплетность термов.

С учётом тонкой структуры схема энергетических уровней выглядит более сложной (мы её не приводим).

Для квантового числа полного момента импульса атома имеется правило отбора

(6.5.20)

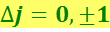
В связи с существованием спина электрона естественно возникает вопрос о том, что и у водородного атома уровни с ℓ > 0 должны быть двойными, а спектральные линии – дублетными. Тонкая структура водородного спектра действительно была обнаружена экспериментально.

Обусловленное спином расщепление энергетических уровней является релятивистским эффектом. Релятивистская квантовая теория даёт для расстояния между уровнями тонкой структуры водородного атома значение

(6.5.21)

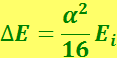
где Ei - энергия ионизации водородного атома,

- «постоянная» тонкой структуры.

Из (6.5.21) следует, что расстояние между уровнями тонкой структуры примерно в 105 раз меньше, чем расстояние между основными уровнями. «Постоянная» тонкой структуры принадлежит к числу фундаментальных констант природы. Она определяет, как сильно электрон связан с электромагнитным полем.

В выражение для α масса электрона не входит. Следовательно, α является константой связи с электромагнитным полем любой элементарной частицы, имеющей заряд е.

к к к