‘»«» ј
В основе нерелятивистской квантовой механики лежит уравнение Шрёдингера:
(6.5.1)
 ,
,
где m – масса частицы;
i – мнимая единица;
U - потенциальная энергия частицы;
Δ - оператор Лапласа, результат действия которого на некоторую функцию представляет собой сумму вторых частных производных по координатам.
В нашем случае:
(6.5.2)
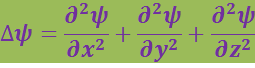 .
.
Уравнение (6.5.1) позволяет найти волновые функции частиц. Из этого уравнения следует, что вид волновой функции определяется функцией U, т.е. в конечном счёте характером сил, действующих на частицу.
Уравнение Шрёдингера является основным уравнением нерелятивистской квантовой механики. Оно не может быть выведено из других соотношений. Его следует рассматривать как исходное основное предположение, справедливость которого доказывается тем, что все вытекающие из него следствия самым точным образом согласуются с опытными фактами.
Если силовое поле, в котором движется частица, стационарно, то функция U не зависит явно от времени t. В этом случае решение уравнения Шрёдингера распадается на два множителя, один из которых зависит только от координат, другой – только от времени:
(6.5.3)
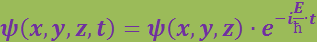 .
.
Здесь Е – полная энергия частицы, которая в случае стационарного поля остается постоянной. Чтобы убедиться в справедливости (6.5.3), подставим его в (6.5.1). В результате получим:
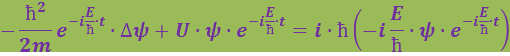
Сократив на общий множитель ![]() , будем иметь:
, будем иметь:
(6.5.4)
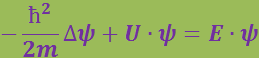 .
.
Перепишем последнее уравнение в виде
(6.5.5)
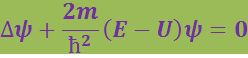
Уравнение (6.5.4) называется уравнением Шрёдингера для стационарных состояний. В дальнейшем мы будем иметь дело только с этим уравнением, в случае стационарного силового поля волновая функция имеет вид (6.5.3). Соответственно
 ,
,
так что плотность вероятности равна ψ* ⋅ ψ и, следовательно, от времени не зависит. По этой причине состояния, описываемые волновыми функциями вида (6.5.3), были названы стационарными.
к к к