ФИЗИКА
Де Бройль связал со свободно движущейся частицей плоскую волну. Реальная плоская, распространявшаяся в направлении оси Х, волна описывается уравнением
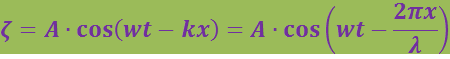
Заменив в соответствии с формулами 
и 
w и λ через E и р, уравнение волны де Бройля для свободной частицы пишут в виде
.
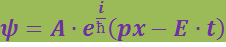Функцию ψ называют волновой функцией (или пси-функцией). Она отражает волновую природу микрочастиц. С её помощью можно описать, например, рассмотренное выше явление дифракции электронов. Для ψ-функции, так же как для световой волны, можно говорить о когерентности, о фазе, о разности хода и других специфических волновых понятиях. Однако в отличие от решения уравнений Максвелла ψ-функция, вообще говоря, комплексна и не имеет наглядного истолкования. Это не реальная бегущая волна типа распространяющегося света или звука и не реальная стоячая волна типа интерференционной картины, а волна (т.е. амплитуда и фаза) вероятности, которая описывает объективно существующие потенциальные возможности осуществления того или иного результата.
Согласно Борну, наглядный смысл имеет только квадрат модуля волновой функции, ψψ*=|ψ|2 который определяет вероятность dp того, что частица будет обнаружена в пределах объема dV:
(6.4.1)
Вот это свойство ψ-функции и отражает вторую (корпускулярную) сторону поведения микрочастиц.
Интеграл от (6.4.1), взятый по всему пространству, должен равняться единице:
(6.4.2)
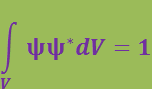
Действительно, этот интеграл дает вероятность того, что частица находится в одной из точек пространства, т.е. вероятность достоверного события, которая равна единице.
Соотношение (6.4.2) носит название условия нормировки. Функции, удовлетворяющие этому условию, называются нормированными.
Из (6.4.1) следует, что квадрат модуля волновой функции дает плотность вероятности (вероятность, отнесенную к единице объема) нахождения частицы в соответствующем месте пространства.
В соответствии со своим смыслом волновая функция должна быть однозначной, непрерывной и конечной. Кроме того, она должна иметь непрерывную и конечную производную. Совокупность перечисленных требований носит название стандартных условий.
Волновая функция удовлетворяет принципу суперпозиции: если система может находиться в различных состояниях, описываемых волновыми функциями ψ1, ψ2,...ψn, то она также может находиться в состоянии ψ, описываемом линейной комбинацией этих функций:
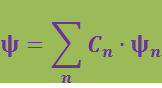
где Сn (n = 1, 2,...) – произвольные, вообще говоря, комплексные числа.
Сложение волновых функций, а не вероятностей, принципиально отличает квантовую теорию от классической статистической теории, в которой для независимых событий справедлива теорема сложения вероятностей.
Из физического смысла волновой функции вытекает, что квантовая механика имеет статический характер. Она не позволяет определить местонахождение частицы в пространстве или траекторию, по которой движется частица. С помощью волновой функции можно лишь предсказать, с какой вероятностью частица может быть обнаружена в различных точках пространства. На первый взгляд может показаться, что квантовая механика дает значительно менее точное описание движения частицы, чем классическая механика, которая «точно» определяет местоположение и скорость частицы в каждый момент времени. Однако в действительности это не так. Квантовая механика гораздо глубже вскрывает истинное поведение микрочастиц. Она лишь не определяет того, чего нет на самом деле.
к к к