ФИЗИКА

6.3.3. Соотношение неопределенностей

Тогда что же такое те следы, которые электроны (и другие заряженные частицы) оставляют в камерах Вильсона, в пузырьковых камерах или в фотоэмульсии? Разве это не изображение траектории? Ведь след очень похож на траекторию. Часто он имеет очень большую длину (тысячи микрон) по сравнению с толщиной (около 0,5 мкм). Он позволяет каждому моменту времени сопоставить определенную область фотопластинки, т.е. казалось бы координаты электрона, а также его энергию, т.е. импульс. И все-таки след это не траектория. В самом деле, посчитаем, с какой точностью можно определить координаты электрона по его следу. «Толщина» следа в фотоэмульсии не может быть меньше диаметра одного проявленного зерна, т.е. 0,5 мкм = 5 · 10-7 м. Это в 5000 раз больше размеров атома и в 100000000 раз больше классического радиуса электрона re = 2,8 ⋅ 10-15 м. Как вы думаете, назвали бы мы с вами траекторией путь пули, если бы его ширина равнялась 100000000 его радиусов, т.е. около 1000 км?! Вероятно, нет, так как «непутёвость» пули здесь вполне очевидна.

Итак, у электрона нет траектории в строгом смысле этого слова. Его положение можно определить лишь приближенно. В нашем мысленном опыте получилось, что при энергии электронов 10 эВ, т.е. при импульсе 3⋅103 эВ/с, неопределённость в его координате Δx составляет 0,66⋅10-10 м. Если перемножить эти две величины, то получится

,

т.е. величина, равная постоянной Планка ħ. Это не случайный результат. Вспомним, что неопределенность в координате Δx равна расстоянию между щелями (и ширине щели δ) и дифракция наблюдается при ширине щели, равной длине волны:

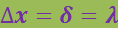
Но λ - это длина волны де Бройля. Она равна , поэтому всегда Δx ⋅ p ≈ ħ. Наконец, сделаем еще одно замечание, прежде чем сформулировать очень важный результат. При прохождении электрона через решётку и попадании его нa фотопластинку импульс электрона может измениться на свою полную величину Δp = p (например, электрон при столкновении с электроном атома решетки может остановиться, так что его импульс будет равен нулю). Таким образом, импульс электрона после прохождения его через пластинку со щелями становится неопределённым. Заменив р на Δp в выражении Δx ⋅ p ≈ ħ, получим универсальное соотношение микромира

(6.3.1)

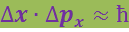
справедливое при любых энергиях электрона.

Это выражение называется соотношением неопределенностей Гейзенберга (принципом неопределенности). Оно отражает специфику свойств микрочастиц, для которых нельзя одновременно точно знать координату и импульс, т.е. нельзя задать траекторию. Чем точнее определяется импульс, тем больше неопределенность в её координате, и наоборот.

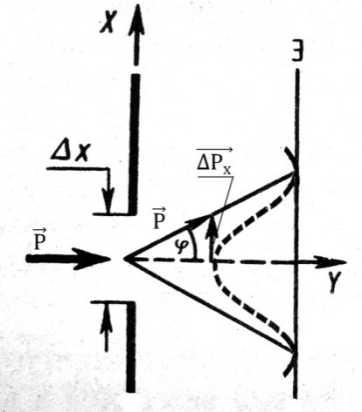
Соотношение (6.3.1) может быть получено также из рассмотрения следующего примера. Попытаемся определить значение координаты Х свободно летящего электрона, поставив на его пути щель шириной ΔX, расположенную перпендикулярно к направлению движения электрона (рис. 6.3.1).

До прохождения электрона через щель его компонента импульса px имеет точное значение, равное нулю (щель по условию перпендикулярна импульсу), так что Δpx = 0, зато координата х электрона является совершенно неопределенной. В момент прохождения электрона через щель положение меняется. Вместо полной неопределенности координаты х появляется неопределенность Δx, но это достигается ценой утраты определенности значения px. Действительно, вследствие дифракции имеется некоторая вероятность того, что частица будет двигаться в пределах угла 2φ, где φ - угол, соответствующий первому дифракционному минимуму (максимумами высших порядков пренебрегаем). Таким образом, появляется неопределенность .

Краю центрального дифракционного максимума (первому минимуму), получающемуся от щели шириной Δx, соответствует угол φ, для которого

.

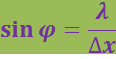Подставляя это значение sinφ в предыдущую формулу, получим:

,

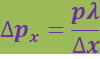или с учетом (6.3.1) будем иметь

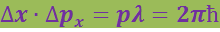
Учет максимумов высших порядков приводит к результату

(6.3.2)

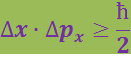
Соотношение (6.3.2) обусловлено корпускулярно-волновой природой электронов (и любых микрочастиц). Оно указывает, в какой мере можно пользоваться понятиями классической механики применительно к микрочастицам, в частности, с какой степенью точности можно говорить о траектории микрочастиц. Движение по траектории характеризуется вполне определенными значениями координат и скорости в каждый момент времени. Подставив вместо px в (6.3.2) произведение mνx, получим соотношение

(6.3.3)

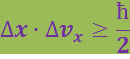
Из (6.3.3) следует: чем больше масса частицы, тем меньше неопределенности ее координаты и скорости, а значит, с тем большей точностью применимо понятие траектории. Уже для макрочастиц размером всего 1 мкм неопределенность значений x и νx оказывается за пределами точности измерения этих величин, так что практически её движение будет неотличимо от движения по траектории.

При определенных условиях даже движение микрочастиц может приближенно рассматриваться как происходящее по траектории. В качестве примера рассмотрим движение электрона в электронно-лучевой трубке.

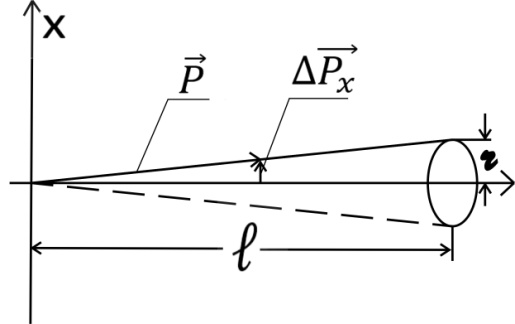
Оценим неопределенность координаты и импульса электрона для этого случая. Пусть след электронного пучка на экране имеет радиус r = 10-2 мм, длина трубки ℓ = 100 мм (рис 6.3.2). Тогда . Импульс электрона связан с ускоряющим напряжением соотношением . Отсюда при напряжении U ~ 104 В энергия электрона равна 104 эВ = 1,65⋅10-15 Дж. Оценим импульс электрона:

Следовательно, Δpx = 5 ⋅ 10-23 ⋅ 10-4 = 5 ⋅ 1027 кг · м/с. Наконец, согласно (6.3.2)

Полученный результат указывает на то, что движение электрона в электронно-лучевой трубке практически неотличимо от движения по траектории.

Соотношение, аналогичное (6.3.2), существует также между энергией частицы и временем измерения этой энергии Δt (или временем жизни частицы):

(6.3.4)

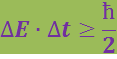
Из (6.3.4) следует, чем больше время жизни частицы, тем точнее определена ее энергия (а значит и масса, так как ), и наоборот.

Энергия электронов в рассмотренном нами мысленном опыте была выбрана 10 эВ, а неопределенность в траектории получилась порядка 10-10 м. Но первое значение характерно для энергии внешних электронов в атоме, а второе – для его размеров. Значит, электроны в пределах атома должны двигаться столь же неопределенно, как и в нашем мысленном эксперименте. К ним нельзя применить обычную механику.

Новая теория, преодолевшая недостатки теории Бора, была создана Гейзенбергом, Шрёдингером и Дираком. Она была названа квантовой (или волновой) механикой. Как сказал кто-то из физиков: «Понять квантовую механику невозможно, к ней можно только привыкнуть». И это очень точно сказано. Квантовую механику нельзя понять, опираясь на классические представления. Это область науки, которую надо строить на совершенно новом фундаменте, на абсолютно новых представлениях.

к к к