ФИЗИКА

6.2.2. Эффект Комптона. Опыт Боте. Фотоны

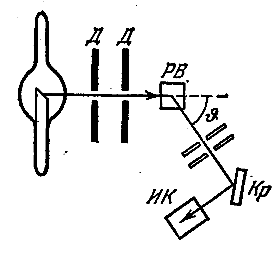
Особенно отчётливо корпускулярные свойства света проявляются в явлении, которое получило название эффекта Комптона. Комптон, исследуя рассеяние рентгеновских лучей различными веществами, обнаружил, что в рассеянных лучах, наряду с излучением первоначальной длины волны λ содержатся также лучи большей длины волны λ'. Разность Δλ = λ' - λ оказалась зависящей только от угла , образуемого направлением рассеянного излучения с направлением первичного пучка. От длины волны λ и от природы рассеивающего вещества Δλ она не зависит. Схема опыта Комптона показана на рис. 6.4.1. Выделяемый диафрагмами Д узкий пучок монохроматического (характеристического) рентгеновского излучения направлялся на рассеивающее вещество РВ.

Спектральный состав рассеянного излучения исследовался с помощью рентгеновского спектрографа, состоящего из кристалла Кр и ионизационной камеры, ИК.

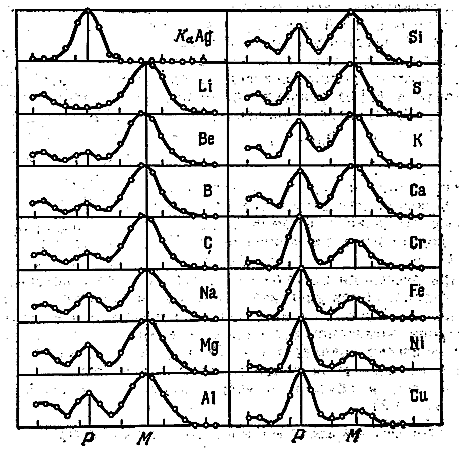
Рис. 6.4.2 характеризует зависимость соотношения интенсивностей смещённой М и несмещённой Р компонент от атомного номера рассеивающего вещества. Верхняя кривая в левом столбце характеризует первичное излучение (линия Kα серебра). При рассеивании веществами с малым атомным номером (Li, Be, B) практически всё рассеянное излучение имеет смещённую длину волны. По мере увеличения атомного номера всё большая часть рассеивается без изменения длины волны.

Все особенности эффекта Комптона можно объяснить, рассматривая рассеяние как процесс упругого столкновения рентгеновских фотонов с практически свободными электронами. Свободными можно считать слабее всего связанные с атомами электроны, энергия связи которых значительно меньше той энергии, которую фотон может передать электрону при соударении.

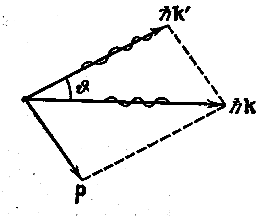
Пусть на первоначально покоящийся свободный электрон падает фотон с энергией и импульсом 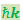(рис. 6.4.3).

Энергия электрона до столкновения равна (m – масса покоя электрона), импульс равен нулю. После столкновения электрон будет обладать импульсом и энергией . Энергия и импульс фотона также изменятся и станут равными и . Из законов сохранения энергии и импульса следует два равенства:

(6.4.1)

;

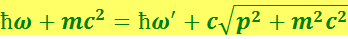(6.4.2)

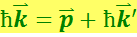
Разделим первое равенство на с. Тогда получим

,

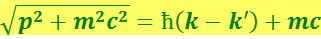где 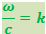. Возведение в квадрат даёт

(6.4.3)

Из (6.4.3) следует, что

(6.4.4)

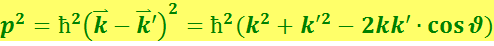
Из сравнения (6.4.3) и (6.4.4) получаем .

Умножим это равенство на 2π и разделим на mckk':

(6.4.5)

Наконец, учтя, что 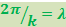, придём к формуле

,

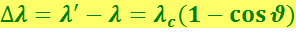где

(6.4.6)

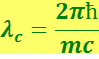
Определяемая выражением (6.4.6) величина 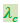называется комптоновской длиной волны той частицы, масса т которой имеется в виду. В рассматриваемом нами случае 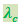- комптоновская длина волны электрона.

При рассеянии фотонов на электронах, связь которых с атомом велика, обмен энергией и импульсом происходит с атомом как целым. Поскольку масса атома намного превосходит массу электрона, комптоновское смещение в этом случае ничтожно и λ' практически совпадает с 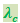. По мере роста атомного номера увеличивается относительное число электронов с сильной связью, чем обусловливается ослабление смещённой линии.

Чтобы объяснить распределение энергии в спектре равновесного теплового излучения, достаточно, как показал Планк, допустить, что свет только испускается порциями . Для объяснения фотоэффекта достаточно предположить, что свет поглощается такими же порциями. Эйнштейн пошёл дальше. Он выдвинул гипотезу, что свет и распространяется в виде дискретных частиц, названных первоначально световыми квантами. Впоследствии эти частицы получили название фотонов.

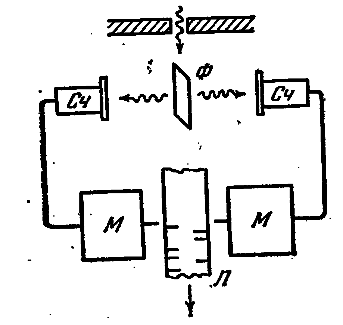
Наиболее непосредственное подтверждение гипотезы Эйнштейна дал опыт Боте. Тонкая металлическая фольга Ф (рис. 6.4.4) помещалась между двумя газоразрядными счётчиками Сч. Фольга освещалась слабым пучком рентгеновских лучей, под действием которых она сама становилась источником рентгеновских лучей (это явление называется рентгеновской флуоресценцией). Вследствие малой интенсивности первичного пучка количество квантов, испускаемых фольгой, было невелико. При попадании в счётчик рентгеновских лучей он срабатывал и приводил в действие механизм М, делавший отметку на движущейся ленте Л. Если бы излучаемая энергия равномерно распространялась во все стороны, как это следует из волновых представлений, оба счётчика должны были бы срабатывать одновременно, и отметки на ленте приходились бы одна против другой. В действительности же наблюдалось совершенно беспорядочное расположение отметок. Это можно объяснить лишь тем, что в отдельных актах испускания возникают световые частицы, летящие то в одном, то в другом направлении.

Так было экспериментально доказано существование особых световых частиц – фотонов. Энергия фотона определяется его частотой:

(6.4.7)

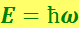
Из теории относительности следует, что:

1) масса покоя фотона равна нулю;

2) фотон всегда движется со скоростью света с;

3) импульс фотона

(6.4.8)

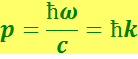
где (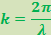 - волновое число). Фотон летит в направлении электромагнитной волны.

Пусть на поглощающую свет поверхность падает поток фотонов, летящих по нормали к поверхности. Если плотность фотонов равна п, на единицу поверхности падает в единицу времени nс фотонов. При поглощении каждый фотон сообщает стенке импульс 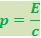(формула 6.4.8). Умножив р на nс, получим импульс, сообщаемый в единицу времени единице поверхности, т.е. давление P света на стенку:

(6.4.9)

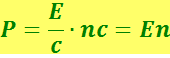
Произведение Е⋅n  равно энергии фотонов, заключённых в единице объёма, т.е. плотности электромагнитной энергии ω. Таким образом, мы пришли к формуле P=ω,  которая совпадает с выражением для давления, получающимся из электромагнитной теории. Отражаясь от стенки, фотон сообщает ей импульс 2р. Поэтому для отражающей поверхности давление будет 2ω.

Итак, мы рассмотрели ряд явлений, в которых свет ведёт себя как поток частиц (фотонов). Однако не надо забывать, что такие явления, как интерференция и дифракция света, могут быть объяснены только на основе волновых представлений. Таким образом, свет обнаруживает корпускулярно-волновой дуализм (двойственность): в одних явлениях проявляется его волновая природа, и он ведёт себя как электромагнитная волна, в других явлениях проявляется корпускулярная природа света, и он ведёт себя как поток фотонов.

Выясним, в каком соотношении находятся волновая и корпускулярная картина. Ответ на этот вопрос можно получить, рассмотрев с обеих точек зрения освещённость какой-либо поверхности. Согласно волновым представлениям, освещённость в некоторой точке поверхности пропорциональна квадрату амплитуды световой волны. С корпускулярной точки зрения освещённость пропорциональна плотности потока фотонов. Следовательно, между квадратом амплитуды световой волны и плотностью потока фотонов имеется прямая пропорциональность. Носителем энергии и импульса является фотон. Квадрат амплитуды волны определяет вероятность того, что фотон попадает в данную точку поверхности. Точнее, вероятность dp того, что фотон будет обнаружен в пределах объёма dV, заключающего в себе рассматриваемую точку пространства, определяется выражением

,

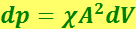где 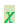– коэффициент пропорциональности;

А – амплитуда световой волны.

Из сказанного следует, что распределение фотонов по поверхности, на которую падает свет, должно иметь статистический характер. Наблюдаемая в опыте равномерность освещённости обусловлена тем, что обычно плотность потока фотонов бывает очень большой. Так, например, при освещённости, равной 50 лк (такая освещённость нужна, чтобы глаза не утомлялись при чтении), и длине волны 5500 E на 1 см2 поверхности падает примерно 2⋅1013 фотонов в секунду. Относительная флуктуация обратно пропорциональна квадратному корню из числа частиц. Поэтому при указанном значении потока фотонов флуктуации оказываются ничтожными, и поверхность представляется освещённой равномерно.

к к к