ФИЗИКА

6.2.1. Законы и природа внешнего фотоэффекта

Внешним фотоэффектом называется испускание электронов веществом под действием света. Это явление было открыто Г. Герцем в 1887 г. Он заметил, что проскакивание искры между шариками разрядника значительно облегчается, если один из шариков осветить ультрафиолетовыми лучами.

Позднее фотоэффект изучался многими учёными. Отметим, прежде всего, работы А.Г. Столетова, Ленарда и Томсона.

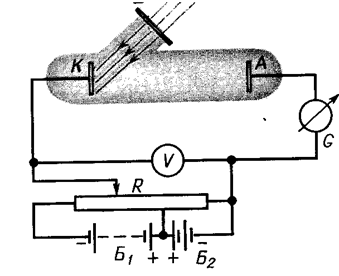
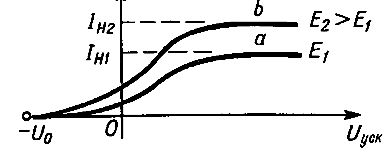
Экспериментальные исследования внешнего фотоэффекта у металлов показали, что он зависит не только от химической природы металла, но и от состояния его поверхности. Даже ничтожные загрязнения поверхности металла существенно влияют на эмиссию электронов под действием света. Поэтому в современных условиях для изучения фотоэффекта пользуются вакуумной трубкой (рис. 6.3.1). Катод К, покрытый исследуемым металлом, освещается монохроматическим светом, проходящим в трубку через окно D. Напряжение U между анодом и катодом регулируется потенциометром R и измеряется вольтметром V. Две аккумуляторные батареи, включённые «навстречу друг другу», позволяют с помощью потенциометра изменять значение и знак напряжения U. Сила фототока измеряется гальванометром G. На рис. 6.3.2 изображены кривые зависимости силы фототока от напряжения Uуск , соответствующие различным потокам света Ф. Частота света в обоих случаях одинакова.

Существование фототока в области отрицательных напряжений от 0 до -U объясняется тем, что фотоэлектроны, выбитые светом из катода, обладают отличной от нуля начальной кинетической энергией. За счёт уменьшения этой энергии электроны могут совершать работу против сил задерживающего электрического поля в трубке и достигать анода. Очевидно, что максимальная начальная скорость νmax фотоэлектронов связана с U0 соотношением

(6.3.1)

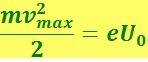
где е и т – абсолютные значения заряда и масса электрона.

При U ≤ -U0 фототок I = 0. По мере увеличения U фототок I постепенно возрастает, так как всё большее число фотоэлектронов достигает анода. Максимальное значение силы тока I= называется фототоком насыщения и соответствует таким значениям U, при которых все электроны, выбиваемые из катода, достигают анода:

,

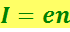где n – число фотоэлектронов, вылетающих из катода за 1 с.

Законы и квантовая теория внешнего фотоэффекта. Опытным путём установлены следующие законы внешнего фотоэффекта:

1. Максимальная начальная скорость фотоэлектронов определяется частотой света и не зависит от его интенсивности.
2. Для каждого вещества существует красная граница фотоэффекта, т.е. минимальная частота ν0 света, при которой ещё возможен внешний фотоэффект (ν0 зависит от химической природы вещества и состояния его поверхности).
3. Число фотоэлектронов n, вырываемых из катода за единицу времени, пропорционально интенсивности света.

Опыты показывают, что фотоэффект практически безынерционен.

При объяснении первого и второго законов встретились серьёзные трудности. В самом деле, согласно электромагнитной теории, вырывание свободных электронов из металла должно являться результатом их «раскачивания» в электрическом поле световой волны. Однако в таком случае совершенно непонятно, почему максимальная начальная скорость и кинетическая энергия вылетающих фотоэлектронов зависят от частоты света, а не от амплитуды колебаний вектора напряжённости электрического поля волны и связанной с ней интенсивности волны. Трудности в истолковании первого и второго законов фотоэффекта вызвали сомнения в универсальной применимости волновой теории света.

В 1905 г. А.Эйнштейн показал, что все закономерности фотоэффекта легко объясняются, если предположить, что свет поглощается такими же порциями ħω (квантами), какими он, по предположению Планка, испускается. По мысли Эйнштейна, энергия, полученная электроном, доставляется ему в виде кванта ħω, который усваивается им целиком. Часть этой энергии, равная работе выхода А, затрачивается на то, чтобы электрон мог покинуть тело. Если электрон освобождается светом не у самой поверхности, а на некоторой глубине, то часть энергии, равная E', может быть потеряна вследствие случайных столкновений в веществе. Остаток энергии образует кинетическую энергию Ek электрона, покинувшего вещество. Энергия Ek будет максимальна, если E' = 0. В этом случае должно выполняться соотношение

(6.3.2)

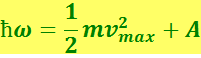
которое называется формулой Эйнштейна.

Уравнение (6.3.2) позволяет легко объяснить все основные законы внешнего фотоэффекта для металлов. Действительно, из него следует, что максимальная кинетическая энергия фотоэлектрона зависит не от интенсивности, а от частоты света и работы выхода А. Внешний фотоэффект возможен только в том случае, когда энергия фотона ħω(hν) больше или, в крайнем случае равна А. Следовательно, соответствующая красной границе фотоэффекта частота

(6.3.3)

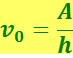
Она зависит только от работы выхода электрона, т.е. от химической природы металла и состояния его поверхности.

Наконец, из явления внешнего фотоэффекта ясно, что общее число n фотоэлектронов, вылетающих за единицу времени, пропорционально числу фотонов n', падающих за то же время на поверхность вещества, которое, в свою очередь, пропорционально интенсивности света.

С изобретением лазеров были получены недостижимые до тех пор мощности световых пучков. Это дало возможность осуществить многофотонные процессы. В частности, был наблюдён многофотонный фотоэффект, в ходе которого электрон, вылетающий из металла, получает энергию не от одного, а от N фотонов (N = 2, 3, 4, 5). Формула Эйнштейна в случае многофотонного эффекта выглядит следующим образом:

(6.3.4)

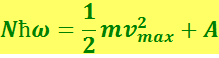
Соответственно красная граница фотоэффекта смещается в сторону более длинных волн (λ увеличивается в N раз).

На основе соотношений (6.3.1) и (6.3.3) уравнение (6.3.2) можно переписать в виде:

(6.3.5)

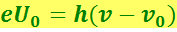
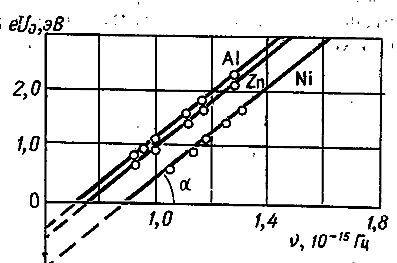
Это уравнение неоднократно подвергалось экспериментальной проверке. На рис. 6.3.3 изображены результаты измерений максимальной кинетической энергии фотоэлектронов как функции частоты облучающего металл света для Al, Zn и Ni. Существенно, что в согласии с уравнением (6.3.4) эти прямые параллельны друг другу, причём производная 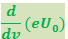не зависит от материала катода и численно равна постоянной Планка. Прямые указывают также на существование граничной частоты ν0 фотоэффекта для данного металла. Отрезки, отсекаемые прямыми на оси ординат, численно равны работе А выхода электронов из соответствующих металлов.

Среднее значение h, полученное из опытов, оказалось равным 6,543⋅10-34 Дж⋅с. Точность опытов составляла 0,1–0,2 %. Совпадение значения h, полученного в опытах по фотоэффекту, с результатами других методов определения подтвердило правильность уравнения (6.3.5) для фотоэффекта и вместе с тем идеи Эйнштейна о квантовом характере взаимодействия света с электронами при фотоэффекте.

к к к