ФИЗИКА

6.1.3. Формулы Рэлея-Джинса и Планка

Формула Рэлея-Джинса. Они рассмотрели равновесное (чёрное) излучение в замкнутой полости с зеркальными стенками как совокупность пространственных стоячих электромагнитных волн. Частоты этих волн должны удовлетворять условиям, подобным условиям для частот стоячих упругих волн в стержнях. Применив теорему о равнораспределении энергии по степеням свободы, им удалось получить формулу, которая имеет вид

(6.1.15)

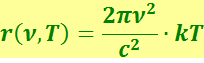или

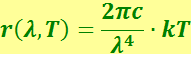
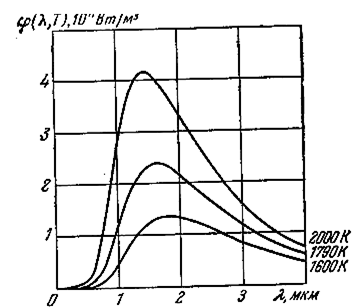
Эта формула удовлетворительно согласуется с экспериментальными данными лишь при больших длинах волн и резко расходится с опытом для малых длин волн. На рис. 6.1.4 сплошной линией изображена экспериментальная кривая, пунктиром – кривая, построенная по формуле Рэлея-Джинса.

С классической точки зрения вывод формулы Рэлея-Джинса является безупречным. Поэтому расхождение этой формулы с опытом указывало на существование каких-то закономерностей, несовместимых с представлениями классической физики.

Невозможность отыскания методами классической теоретической физики такого выражения для функций Кирхгофа, которое согласовывалось бы с данными экспериментов во всём интервале частот от 0 до , получило образное название «ультрафиолетовой катастрофы».        

Формула Планка. Выход из трудностей, возникших в проблеме теплового излучения абсолютно чёрного тела, был предложен Планком в 1900 г. Уподобив равновесное излучение совокупности линейных гармонических осцилляторов со всевозможными собственными частотами от нуля до бесконечности, Планк пытался применить термодинамический подход для нахождения функции Кирхгофа. Ему удалось подобрать эмпирическое выражение, которое блестяще согласовывалось с экспериментальными данными (рис. 6.1.4 – сплошная кривая) при любой частоте и температуре.

Для теоретического обоснования этой формулы Планку пришлось сделать предположение, совершенно чуждое классическим представлениям, а именно, допустить, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), величина которых пропорциональна частоте излучения:

(6.1.16)

,

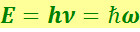где 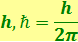– коэффициенты пропорциональности, получившие название постоянной Планка (, ).

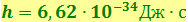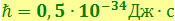В механике есть величина, имеющая размерность «энергия×время», которая называется действием. Поэтому постоянную Планка иногда называют квантом действия. Заметим, что размерность 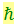совпадает с размерностью момента импульса.

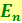Если излучение испускается порциями , то его энергия должна быть кратна этой величине:

(6.1.17)

Не вдаваясь в подробности вывода, приведём формулу Планка

(6.1.18)

.

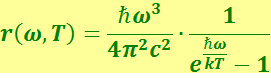Осуществив преобразование выражения (6.1.18) по формуле (6.1.4), будем иметь

(6.1.19)

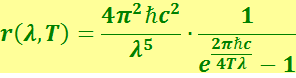
Поскольку формула Планка справедлива при любых частотах и температурах, то из неё должны следовать все известные законы теплового излучения.

Получим с учётом (6.1.18) закон Стефана-Больцмана:

(6.1.20)

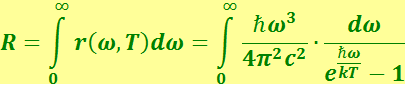
Введём вместо ω безразмерную переменную 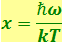. Подстановка 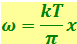и преобразует формулу (6.1.20) к виду

(6.1.21)

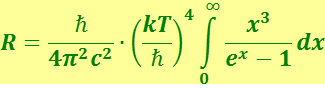
Определённый интеграл в (6.1.21) равен 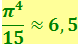 . Подставив его значение в (6.1.21), получим закон Стефана-Больцмана:

.

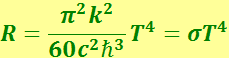Подстановка в эту формулу значений k, c и 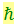даёт 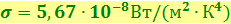, что хорошо согласуется с экспериментальным значением.

В заключение найдём значение постоянной в законе смещения Вина. Для этого продифференцируем функцию (6.1.19) по λ  и приравняем получившееся выражение нулю:

.

Удовлетворяющие этому уравнению значения λ = 0 и λ = ∞ соответствуют минимумам функции r(λ, T). Значение λm, при котором функция достигает максимума, обращает в нуль выражение, стоящее в числителе в квадратных скобках. Обозначив 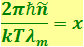, получим уравнение .

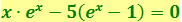Решение этого трансцендентного уравнения даёт x = 4,965. Следовательно, 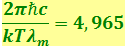, откуда  .

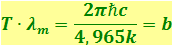Подстановка числовых значений 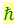, с и k даёт для b величину, совпадающую с экспериментальным значением.

Таким образом, формула Планка даёт исчерпывающее описание равновесного теплового излучения.

к к к