ФИЗИКА

3.3.1. Энергия системы точечных зарядов

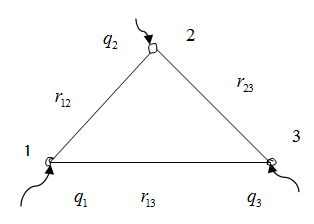
Было показано (п. 3.1.9), что кулоновские силы консервативны. Следовательно, система точечных зарядов q1, q2,...,qN обладает взаимной потенциальной энергией. Чтобы найти выражение для этой энергии, предположим, что заряды последовательно перемещаются из бесконечности в соответствующие точки поля (рис. 3.3.1).

Начнём с заряда q1. Перенесение его из бесконечности в точку 1 не требует совершения работы, поскольку остальные заряды удалены от него на бесконечность и с ним не взаимодействуют .

Для перенесения заряда 2 из бесконечности в точку 2 нужно совершить работу против сил поля, созданного зарядом q1. Согласно формуле (3.1.53) эта работа равна произведению q2 на потенциал поля, создаваемого зарядом q1 в точке 2:

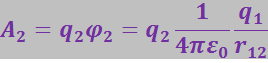
Для перенесения заряда q3 из бесконечности в точку 3 надо совершить работу, равную произведению q3 на потенциал поля, создаваемого зарядами q1 и q2 в точке 3:

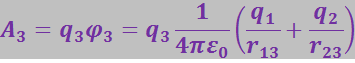
Сумма работ даст энергию системы трёх зарядов:

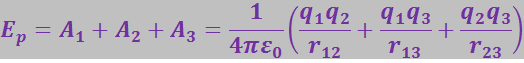
Учтя, что, например, , полученной формуле можно придать симметричный вид:

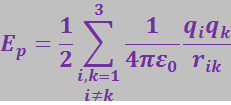
При суммировании индексы i и k пробегают независимо друг от друга значения 1, 2, 3; слагаемые у которых i = k исключаются.

Можно убедиться в том, что аналогичная формула получается для системы любого числа N точечных зарядов:

(3.3.1)

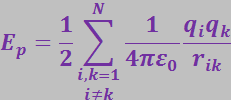
Учтя, что

,

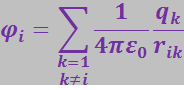получим:

(3.3.2)

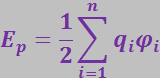
к к к