ФИЗИКА
Как видно из предыдущего примера, ёмкость уединённых проводников невелика. Вместе с тем в технике бывают нужны устройства, которые при небольшом потенциале накапливали бы на себе большие заряды.
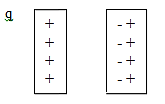
В основу таких устройств, называемых конденсаторами, положен тот факт, что ёмкость проводника возрастает при приближении к нему другого проводника. Это вызвано тем, что под действием поля, создаваемым заряженным проводником, на находящемся поблизости незаряженном проводящем теле возникают индуцированные заряды. При этом индуцированный заряд q на проводнике, располагается ближе к проводнику, чем одноимённый с q индуцированный заряд (рис. 3.2.13) и, следовательно, согласно (3.1.50) оказывает большое влияние на его потенциал. Поэтому при поднесении к заряженному проводнику незаряженного проводящего тела потенциал проводника уменьшается. Согласно формуле (3.2.34) это означает увеличение ёмкости проводника.
Рис. 3.2.13 |
Конденсаторы делают в виде двух проводников (называемых обкладками), помещённых близко друг к другу. Для того, чтобы внешние тела не влияли на ёмкость конденсатора, обкладкам придают такую форму и так располагают их друг относительно друга, чтобы поле, создаваемое накапливаемыми на них зарядами, было сосредоточено внутри конденсатора. Этому условию удовлетворяют две пластинки, расположенные близко друг к другу, два коаксиальных цилиндра и две концентрические сферы. Соответственно бывают плоские, цилиндрические и сферические конденсаторы.
Ёмкостью конденсатора называют величину С, пропорциональную заряду q, находящемуся на одной из обкладок (на другой находится заряд -q), и обратно пропорциональную разности потенциалов между обкладками:
(3.2.36)
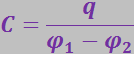
Разность потенциалов 
называют напряжением между соответствующими точками. Поэтому формулу (3.2.36) можно представить в виде
(3.2.37)
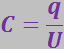
где U – напряжение между обкладками.
Ёмкость конденсаторов измеряется в тех же единицах, что и ёмкость уединённых проводников.
Найдём ёмкость плоского конденсатора. Пусть площадь обкладки равна S, а расстояние между обкладками d. Зазор между обкладками предполагается заполненным диэлектриком с проницаемостью ε. Если d много меньше линейных размеров обкладок, в подавляющей части объёма поле будет таким, как поле двух бесконечных разноимённых заряженных плоскостей.
Поэтому мы не внесём существенной погрешности, если будем поле во всём объёме конденсатора вычислять по формуле (3.1.38), подставив вместо σ отношение заряда q, находящегося на обкладке, к площади обкладки S. Приняв, что диэлектрик ослабляет поле в ε раз, получим для напряжённости поля в диэлектрике выражение:
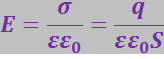
Согласно формуле (3.1.57) напряжение между обкладками
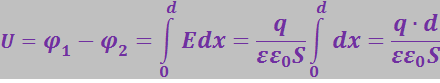
(ось х перпендикулярна обкладкам). Отсюда для ёмкости плоского конденсатора получим:
(3.2.38)
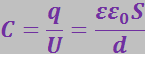
Аналогичный расчёт для цилиндрического конденсатора даёт
(3.2.39)
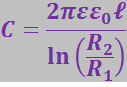
где ℓ – длина обкладок цилиндрического конденсатора;
R2 и R1 – соответственно радиусы внешнего и внутреннего цилиндров.
Ёмкость сферического конденсатора определяется выражением
(3.2.40)
где R1 и R2 – радиусы внутренней и внешней обкладок.
Из выражений (3.2.38), (3.2.39) и (3.2.40) ясно, почему введение между обкладками прослойки из сегнетоэлектрика позволяет получить при небольших размерах конденсаторов значительную ёмкость.
Располагая набором конденсаторов, можно получить много различных значений ёмкости, если применить соединение конденсаторов в батареи.
При этом надо учитывать, что при параллельном соединении n конденсаторов
(3.2.41)
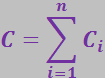
где С – общая ёмкость батареи, а при последовательном соединении:
(3.2.42)
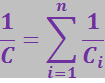
к к к