ÔÈÇÈÊÀ
Сообщённый проводнику заряд q распределяется по его поверхности так, чтобы напряжённость поля внутри проводника была равна нулю. Такое распределение является единственным. Поэтому, если проводнику уже несущему заряд q, сообщить ещё заряд такой же величины, то второй заряд должен распределиться по проводнику точно таким же образом, как и первый, в противном случае он создаёт в проводнике поле, отличное от нуля. Следует оговорить, что это справедливо лишь для удалённого от других тел (уединённого) проводника. Если вблизи данного проводника находятся другие тела, сообщение проводнику новой порции заряда вызовет изменение поляризации этих тел, либо изменение индуцированных зарядов на этих телах. В результате подобие в распределении различных порций заряда будет нарушено.
Итак, различные по величине заряды распределяются на уединённом проводнике подобным образом (отношение плотностей заряда в двух произвольных точках поверхности проводника при любой величине заряда будет одним и тем же).
Отсюда вытекает, что потенциал уединённого проводника пропорционален находящемуся на нём заряду. Действительно, увеличение в некоторое число раз заряда приводит к увеличению в то же число раз напряжённости поля в каждой точке окружающего проводник пространства. Соответственно в такое же число раз возрастёт работа переноса единичного заряда из бесконечности на поверхность проводника, т.е. потенциал проводника. Таким образом, для уединённого проводника
(3.2.33)
Коэффициент пропорциональности С между потенциалом и зарядом называется электроёмкостью (или просто ёмкостью) проводника. Из (3.2.33) следует, что
(3.2.34)
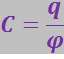
В соответствии с (3.2.34) ёмкость численно равна заряду, сообщение которого проводнику повышает его потенциал на единицу.
Найдём ёмкость шара радиуса R, погружённого в безграничный однородный и изотропный диэлектрик с проницаемостью ε. Воспользовавшись формулой (3.1.57), вычислим потенциал φ, который приобретает шар после сообщения ему заряда q:
.
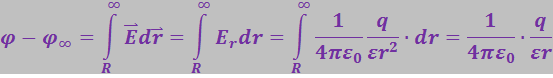Положив потенциал на бесконечности 
равным нулю, получим:
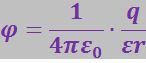
Отсюда
(3.2.35)
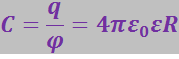
Итак, ёмкость уединённого шара пропорциональна его радиусу и диэлектрической проницаемости среды.
За единицу ёмкости принимается ёмкость такого проводника, потенциал которого изменяется на 1 В при сообщении ему заряда 6 Кл. Эта единица называется фарадом (Ф).
Фарад очень большая величина. Поэтому на практике используют дольные единицы: миллифарад (
), микрофарад (
), нанофарад (
) и пикофарад (
).
Если вычислить электроёмкость Земли, как ёмкость проводимого шара, радиус которого равен 6400 км, то она оказывается равной только 711 мкФ.
ê ê ê