ФИЗИКА
3.2.5. Поле внутри плоской пластины
Рассмотрим две бесконечные параллельные разноимённо заряженные плоскости. Пусть создаваемое ими в вакууме поле характеризуется напряжённостью ![]() и смещением
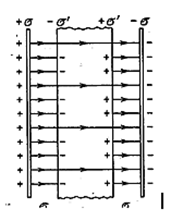
и смещением ![]() . Внесём в это поле пластину из однородного изотропного диэлектрика и расположим её так, как показано на рис. 3.2.6.
. Внесём в это поле пластину из однородного изотропного диэлектрика и расположим её так, как показано на рис. 3.2.6.
Рис. 3.2.6 |
Под действием поля диэлектрик поляризуется, и на его поверхностях появятся связанные заряды плотности σ'. Эти заряды создадут внутри пластины однородное поле, напряжённость которого согласно формуле (3.1.38) равна ![]() . Вне диэлектрика в данном случае
. Вне диэлектрика в данном случае ![]() . Напряжённость поля
. Напряжённость поля ![]() . Оба поля направлены навстречу друг другу, следовательно, внутри диэлектрика
. Оба поля направлены навстречу друг другу, следовательно, внутри диэлектрика
(3.2.25)

Вне диэлектрика ![]() .
.
Поляризация диэлектрика обусловлена полем (3.2.25). Это поле перпендикулярно к поверхностям пластины, поэтому ![]() и в соответствии с (3.2.7)
и в соответствии с (3.2.7) ![]() . Подставив это значение в (3.2.25), получим:
. Подставив это значение в (3.2.25), получим:
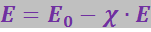
откуда
(3.2.26)
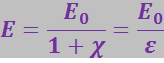
Итак, диэлектрическая проницаемость ε показывает, во сколько раз ослабляется поле в диэлектрике.
Умножив (3.2.26) на εε0, получим электрическое смещение внутри пластины
(3.2.27)

Таким образом, электрическое смещение внутри пластины совпадает с электрическим смещением внешнего поля ![]() . Заменив в (3.2.27)
. Заменив в (3.2.27) ![]() через
через ![]() , получим, что
, получим, что
(3.2.28)

Чтобы найти σ', выразим в (3.2.26) E и ![]() через плотности зарядов
через плотности зарядов
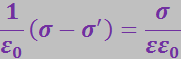
Отсюда
(3.2.29)
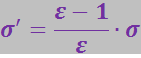
Рис. 3.2.6 выполнен в предположении, что ε = 3. В соответствии с этим густота линий ![]() в диэлектрике в три раза меньше, чем вне пластины. Линии проведены на одинаковых расстояниях друг от друга, поскольку поле однородно. В данном случае σ' можно найти из рис. 3.2.6. Действительно, разряжённость поля внутри пластины в три раза меньше, чем вне её, то из трёх линий напряжённости, начинающихся (или заканчивающихся) на сторонних зарядах, две должны заканчиваться (или начинаться) на связанных зарядах. Отсюда вытекает, что плотность связанных зарядов должна быть равна 2/3 плотности сторонних зарядов.
в диэлектрике в три раза меньше, чем вне пластины. Линии проведены на одинаковых расстояниях друг от друга, поскольку поле однородно. В данном случае σ' можно найти из рис. 3.2.6. Действительно, разряжённость поля внутри пластины в три раза меньше, чем вне её, то из трёх линий напряжённости, начинающихся (или заканчивающихся) на сторонних зарядах, две должны заканчиваться (или начинаться) на связанных зарядах. Отсюда вытекает, что плотность связанных зарядов должна быть равна 2/3 плотности сторонних зарядов.
к к к