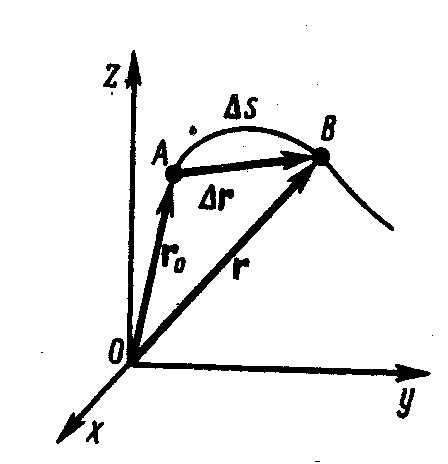ФИЗИКА

1.1.1. Кинематика материальной точки

Существует три способа описания движений точки. Мы рассмотрим два из них: векторный и координатный.

Векторный способ. В этом способе положение интересующей нас материальной точки А задают радиусом-вектором , проведённым из некоторой неподвижной точки О выбранной системы отсчёта в точку А (рис. 1.1.1).

При движении материальной точки А её радиус-вектор меняется в общем случае как по модулю, так и по направлению, т.е. радиус-вектор 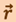зависит от времени t. Геометрическое место концов радиус-вектора 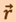называют траекторией точки А. Длина участка траектории 1-2, пройденного материальной точкой, называется длиной пути . является скалярной функцией времени 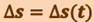. Вектор называется вектором перемещения. Он представляет собой приращение радиуса вектора 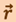за время перемещения :

.

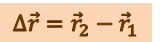Для характеристики быстроты движения и его направления вводится векторная величина – скорость.

Вектором средней скорости называется отношение вектора перемещения к промежутку времени :

(1.1.1)

.

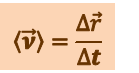Вектор совпадает по направлению с .

При неограниченном уменьшении средняя скорость стремится к предельному значению, которое называется мгновенной скоростью :

(1.1.2)

.

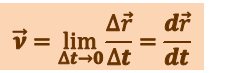Так как секущая в пределе совпадает с касательной, то вектор скорости направлен по касательной к траектории в сторону движения (рис. 1.1.2).

Модуль мгновенной скорости определяется соотношением:

(1.1.3)

.

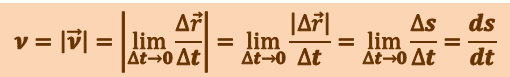При неравномерном движении модуль мгновенной скорости с течением времени изменяется. В этом случае пользуются скалярной величиной 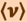- средней скоростью неравномерного движения:

(1.1.4)

.

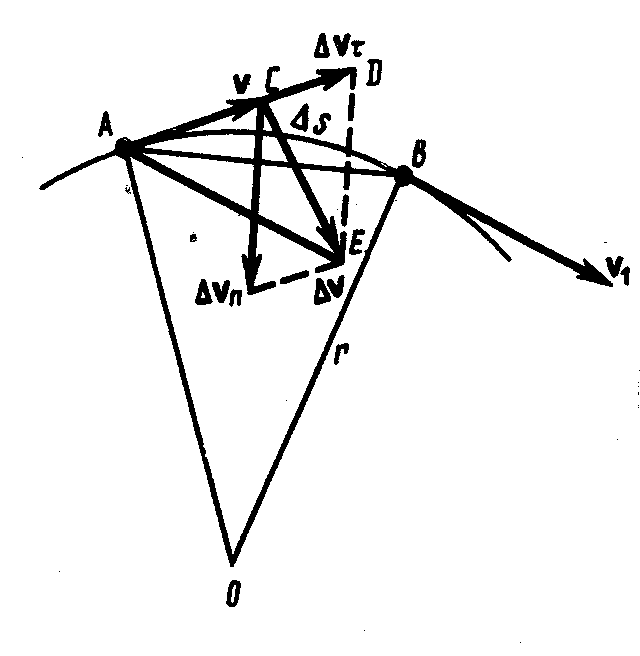
Ускорение и его составляющие. В случае неравномерного движения важно знать, как быстро изменяется скорость с течением времени. Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является Рассмотрим плоское движение, т.е. движение при котором все участки траектории точки лежат в одной плоскости. Пусть вектор задаёт скорость точки А в момент времени t. За время движущаяся точка перешла в положение В и приобрела скорость, отличную от как по модулю, так и по направлению и равную .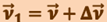

Перенесём вектор 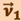в точку А и найдём (рис. 1.1.2).

Средним ускорением неравномерного движения в интервале от t до Δt, называется векторная величина, равная отношению изменения скорости 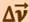к интервалу времени :

(1.1.5)

.

Мгновенным ускорением 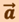материальной точки в момент времени t будет предел среднего ускорения:

(1.1.6)

.

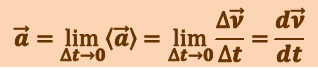Таким образом, ускорение есть векторная величина, равная первой производной скорости по времени.

Разложим вектор 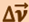на две составляющие. Для этого из точки А (рис. 1.1.2) по направлению скорости отложим вектор АД, по модулю равный 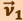. Очевидно, что вектор 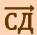, равный 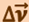, определяет изменение скорости за время по модулю 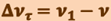. Вторая же составляющая 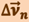вектора 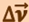характеризует изменение скорости за время по направлению.

Тангенциальная составляющая ускорения

(1.1.7)

,

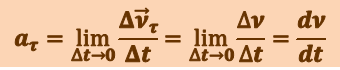т.е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.

Найдём вторую составляющую ускорения. Допустим, что точка В достаточно близка к точке А, поэтому можно считать дугой окружности некоторого радиуса r, мало отличающейся от хорды АВ. Тогда из подобия треугольников АОВ и ЕАД следует 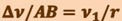, но так как 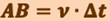, то

.

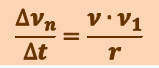В пределе при ∆t → 0 получим . Поскольку угол ЕАД стремится к нулю, а так как треугольник ЕАД равнобедренный, то угол между и 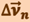стремится к прямому. Следовательно, при ∆t → 0 векторы 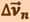и оказываются взаимно перпендикулярными. Так как вектор скорости направлен по касательной к траектории, то вектор 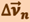направлен к центру её кривизны. Вторая составляющая ускорения, равная

(1.1.8)

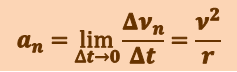
называется нормальной составляющей ускорения и направлена по нормали к траектории к центру её кривизны.

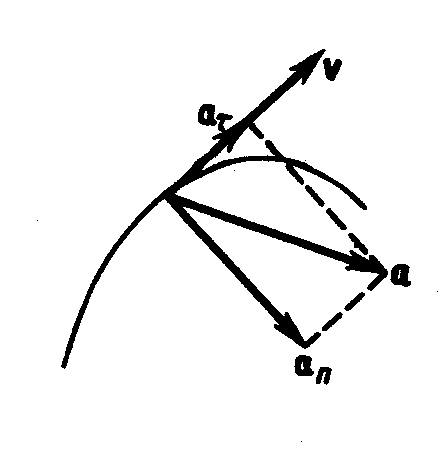
Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис. 1.1.3)

(1.1.9)

;

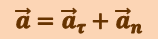(1.1.10)

.

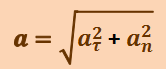Таким образом, зная зависимость 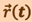, можно, используя вышеприведённые соотношения, найти скорость и ускорение 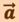материальной точки в каждый момент времени. Это прямая задача кинематики.

Возникает и обратная задача: можно ли найти и 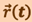, зная зависимость от времени ускорения ?

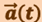Оказывается, для получения однозначного решения этой задачи одной зависимости 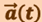недостаточно, необходимо ещё знать так называемые начальные условия, а именно скорость и радиус-вектор точки в некоторый начальный момент t = 0. Чтобы в этом убедиться, рассмотрим простейший случай, когда в процессе движения ускорение точки .

Сначала определим скорость точки . Согласно (1.6), за промежуток времени dt элементарное приращение скорости 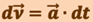, найдём приращение вектора скорости за это время:

.

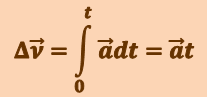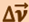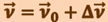Но величина - это ещё не искомая скорость . Чтобы найти , необходимо знать скорость в начальный момент времени. Тогда , или

(1.1.11)

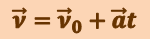
Аналогично решается вопрос и о радиус-векторе 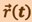точки. Согласно (1.1.2), за промежуток времени элементарное приращение радиус-вектора 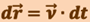. Интегрируя это выражение с учётом (1.1.11), определим приращение радиуса-вектора за время от t = 0 до t:

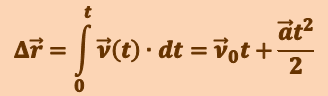
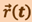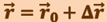Для нахождения самого радиус-вектора необходимо знать ещё положение точки в начальный момент времени. Тогда , или

.

Координатный способ. В этом способе с телом отсчёта жёстко связывают определённую систему координат. На рис. 1.1.1 с телом отсчёта связана, декартова система координат x, y, z.

Запишем проекции на оси x, y, z радиус-вектора 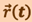, характеризующего положение интересующей нас точки А относительно начала координат О в момент t:

.

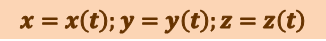Зная зависимости этих координат от времени – закон движения точки, можно найти положение точки в каждый момент времени, её скорость и ускорение. Действительно, спроектировав (1.1.2) и (1.1.6), например, на ось х, получим формулы, определяющие проекции векторов скорости и ускорения на эту ось:

(1.1.12)

,

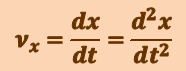где dx - проекция вектора перемещения 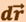на ось х;

(1.1.13)

,

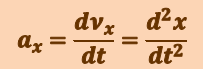где 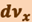- проекция вектора приращения скорости на ось х. Аналогичные соотношения получаются для y- и z-проекций соответствующих векторов. Из этих формул видно, что проекции векторов скорости и ускорения равны соответственно первой и второй производным координат по времени. Зная проекции векторов, можно найти модуль и направление векторов и 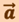в любой момент времени. Например, модуль вектора скорости

,

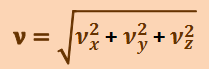направление же вектора задаётся направляющими косинусами

,

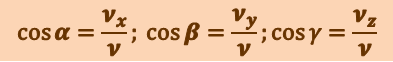где α, β, γ - углы между вектором и осями x, y, z соответственно. Аналогичными формулами определяются модуль и направление вектора ускорения.

Кроме этого можно решить и ряд других вопросов: найти траекторию точки, зависимость пройденного ею пути от времени, зависимость скорости от положения точки и т.д.

Решение обратной задачи – нахождение скорости и закона движения точки по заданному ускорению – проводится, как и в векторном способе, путём интегрирования (в данном случае проекций ускорения по времени), причём задача и здесь имеет однозначное решение, если кроме ускорения заданы ещё и начальные условия: проекции скорости и координаты точки в начальный момент времени.

к к к