ФИЗИКА

3.2.3. Вектор электрического смещения

Связанные заряды, как и другие электрические заряды, являются источниками электрического поля. Поэтому при вычислении поля в диэлектриках, наряду с плотностью ρ сторонних зарядов, нужно учитывать плотность ρ' связанных зарядов. Следовательно, при наличии диэлектриков формула (3.1.35) должна быть написана в виде

(3.2.9)

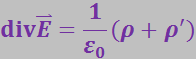
Эта формула непригодна для нахождения вектора , так как она выражает дивергенцию искомой величины через плотность ρ', которая в свою очередь определяется напряжённостью . Получается «заколдованный круг» – чтобы найти , нужно знать ρ', а чтобы найти ρ', нужно знать .

Указанное затруднение можно обойти, введя вспомогательную величину, источниками которой являются только сторонние заряды. Для нахождения этой величины подставим в формулу (3.2.9) выражение (3.2.8) для ρ':

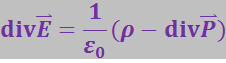
Введём ε0 под знак дивергенции, тогда получим:

(3.2.10)

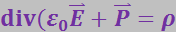
Величину 90

(3.2.11)

называют электрическим смещением поля. Её дивергенция определяется (3.2.10) только плотностью свободных зарядов.

Установим связь между и . Для этого в (3.2.11) подставим выражение (3.2.3):

(3.2.12)

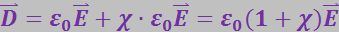
Безразмерную величину

(3.2.13)

называют относительной диэлектрической проницаемостью вещества. В вакууме ε = 1.

С учётом (3.2.13) формулу (3.2.12) можно представить в виде

(3.2.14)

В вакууме:

(3.2.15)

Согласно формулам (3.1.6) и (3.2.15) электрическое смещение поля точечного заряда в вакууме определяется выражением:

(3.2.16)

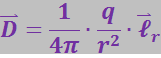
Отсюда следует, что единицей электрического смещения является кулон на квадратный метр (Кл/м2).

Согласно (3.2.10):

(3.2.17)

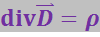
Эта формула выражает теорему Гаусса для вектора в дифференциальной форме.

Чтобы получить теорему Гаусса для в интегральной форме, проинтегрируем соотношение (3.2.17) по произвольному объёму V:

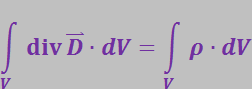
Преобразуем левую часть по теореме Остроградского-Гаусса (3.1.28)

(3.2.18)

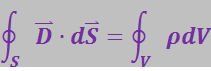
Слева стоит поток вектора через замкнутую поверхность S, справа – суммарный сторонний заряд, заключённый внутри этой поверхности. Если этот заряд образован дискретными точечными зарядами равенство (3.2.18) можно написать в виде

(3.2.19)

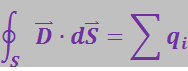
Справа стоит алгебраическая сумма сторонних зарядов, заключённых внутри поверхности S.

Формулы (3.2.18) и (3.2.19) выражают теорему Гаусса для вектора в интегральной форме: поток электрического смещения через замкнутую поверхность равен алгебраической сумме сторонних зарядов, заключённых внутри этой поверхности.

Поле вектора можно изобразить с помощью линий электрического смещения. При этом линии вектора могут начинаться и оканчиваться только на сторонних зарядах.

к к к