ФИЗИКА
3.1.11. Поведение диполя во внешнем электрическом поле
Если диполь поместить в однородное электрическое поле, образующие диполь заряды +q и -q окажутся под действием равных по величине, но противоположных по направлению сил 
и 
(рис. 3.1.29). Эти силы образуют пару, плечо которой равно 
, т.е. зависит от ориентации диполя относительно поля. Модуль каждой из сил равен qE. Умножив его на плечо, получим величину момента пары сил, действующих на диполь:
(3.1.63)
(р – электрический момент диполя). Перепишем (3.1.63) в векторном виде:
(3.1.64)
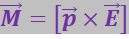
Момент сил (3.1.64) стремится повернуть диполь так, чтобы его электрический момент 
установился по направлению поля.
Рис. 3.1.29 |
Найдём потенциальную энергию, которой обладает диполь во внешнем электрическом поле. Согласно (3.1.51) эта энергия равна:
(3.1.65)
Здесь φ+ и φ- – значения потенциала внешнего поля в тех точках, где помещаются заряды +q и -q.
Потенциал однородного поля убывает линейно в направлении вектора 
. Приняв это направление за ось х (рис. 3.1.30), можно написать, что 
.
Рис. 3.1.30 |
Из рис. 3.1.30 видно, что разность φ+ - φ- равна приращению потенциала на отрезке 
.
Подставив это значение в (3.1.65), получим:
(3.1.66)
или
(3.1.67)
В (3.1.67) не учитывается энергия взаимодействия зарядов, образующих диполь. Мы получили эту формулу, считая для простоты поле однородным. Однако формула (3.1.67) справедлива и для неоднородного поля.
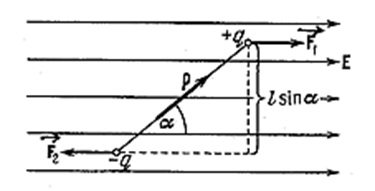
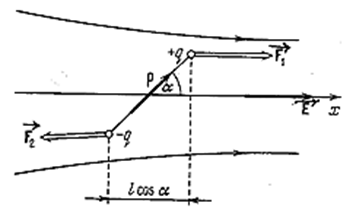
Рассмотрим качественно поведение диполя в неоднородном поле, обладающем симметрией относительно оси х (рис. 3.1.31).
Рис. 3.1.31 |
Пусть центр диполя лежит на этой оси, причём электрический момент диполя образует с осью угол α, отличный от π/2. В этом случае силы, действующие на заряды диполя, не одинаковы по величине. Поэтому, кроме вращательного момента, на диполь будет действовать сила, стремящаяся переместить его в направлении оси х. Соответствующий расчёт даёт
(3.1.68)
Из (1.68) следует, что при α < π/2 величина Fx положительна. Это означает, что под действием силы Fx диполь втягивается в область более сильного поля.
При α > π/2 диполь выталкивается из поля.
к к к