ФИЗИКА
3.1.10. Связь между напряжённостью электростатического поля и потенциалом
Итак, электростатическое поле можно описать либо с помощью векторной величины ![]() , либо с помощью скалярной величины φ. Очевидно, что между этими величинами должна существовать определённая связь.
, либо с помощью скалярной величины φ. Очевидно, что между этими величинами должна существовать определённая связь.
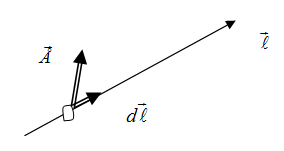
Установим её вид. Для этого выберем в пространстве, в котором имеется электростатическое поле, произвольное направление ℓ (рис. 3.1.25).
Рис. 3.1.25 |
При перемещении точечного заряда q вдоль этого направления на отрезок ![]() силы поля совершают над ним работу
силы поля совершают над ним работу
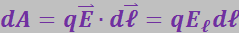
(здесь ![]() – проекция
– проекция ![]() на направление ℓ).
на направление ℓ).
Согласно формуле (3.1.51) эту работу можно выразить через убыль потенциала: ![]() (взята частная производная, поскольку φ, вообще говоря, изменяется не только при перемещении вдоль направления ℓ, но также и при перемещениях в других направлениях). Приравняв оба выражения для работы, получим
(взята частная производная, поскольку φ, вообще говоря, изменяется не только при перемещении вдоль направления ℓ, но также и при перемещениях в других направлениях). Приравняв оба выражения для работы, получим
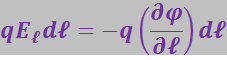 ,
,
откуда после сокращений следует, что
(3.1.54)
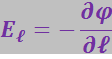
Таким образом, проекция вектора ![]() на направление
на направление ![]() равна скорости убывания потенциала вдоль этого направления.
равна скорости убывания потенциала вдоль этого направления.
Взяв в качестве направления ℓ координатные оси x, y, z получим выражения для компонент вектора ![]() :
:
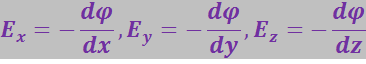
Соответственно выражение для ![]() будет иметь вид
будет иметь вид
(1.55)
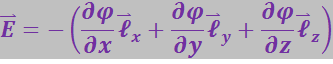
Величина, стоящая в скобках, представляет собой градиент функции φ. Следовательно, мы приходим к формуле
(1.56)
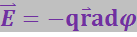
согласно которой напряжённость электростатического поля равна градиенту потенциала, взятому с обратным знаком.
С помощью (3.1.56) можно, зная функцию ![]() , найти напряжённость поля в каждой точке поля. Можно решить и обратную задачу – зная функцию
, найти напряжённость поля в каждой точке поля. Можно решить и обратную задачу – зная функцию ![]() , найти разность потенциалов между двумя произвольными точками поля.
, найти разность потенциалов между двумя произвольными точками поля.
Для этого воспользуемся тем, что работа, совершаемая силами поля над зарядом q при перемещении его из точки 1 в точку 2, может быть вычислена как
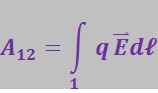
Вместе с тем в соответствии с (3.1.52) та же работа может быть представлена в виде
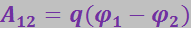
Приравняв друг другу эти два выражения и сократив на q, придём к соотношению:
(3.1.57)
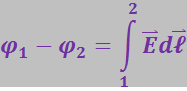
Интеграл можно брать по любой линии, соединяющей точки 1 и 2, ибо работа сил поля не зависит от пути.
В качестве примеров применения соотношения (3.1.57) вычислим разность потенциалов между двумя произвольными точками в некоторых полях, рассмотренных п. 3.1.8.
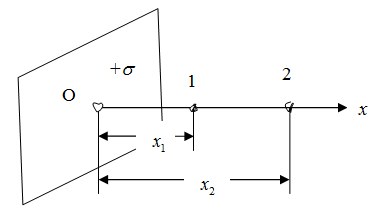
Поле бесконечной однородно заряженной плоскости (рис. 3.1.26). Вычислим разность потенциалов между точками 1 и 2, находящимися на расстояниях ![]() и
и ![]() от плоскости. Поле однородно, поэтому напряжённость поля во всех точках одна и та же и равна
от плоскости. Поле однородно, поэтому напряжённость поля во всех точках одна и та же и равна
(3.1.58)
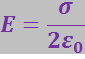
С учётом этого, подставив (3.1.58) в (3.1.57), получим
(3.1.59)
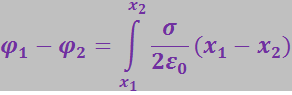
Рис. 3.1.26 |
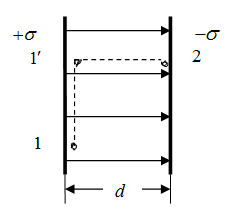
Поле двух разноимённо заряженных бесконечных плоскостей (рис. 3.1.27). Вычислим разность потенциалов между точками 1 и 2, лежащими на плоскостях, расстояние между которыми d. При этом учтём, что поле однородно и согласно (3.1.38) ![]() .
.
Рис. 3.1.27 |
Разобьём путь интегрирования на два участка 1-1' и 1'-2. Тогда
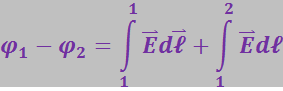
Очевидно, что интеграл на участке 1-1' равен нулю, так как угол между ![]() и
и ![]() равен 90°, а
равен 90°, а ![]() . С учётом этого будем иметь
. С учётом этого будем иметь
(3.1.60)
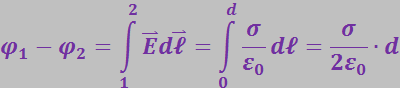
Очевидно, что по такому же (линейному) закону изменяется с расстоянием потенциал в плоском конденсаторе.
Цилиндрический конденсатор. Рассмотрим распределение потенциала между коаксиальными цилиндрами. Напряжённость этого поля выражается формулой (3.1.40). Поэтому разность потенциалов между точкой 1, лежащей на внутреннем цилиндре и произвольной точкой 2 между электродами равна
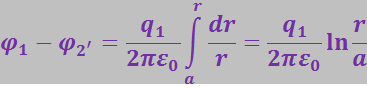
Здесь r – расстояние от рассматриваемой точки до оси цилиндра; а – радиус внутреннего цилиндра; q1 – заряд внутреннего цилиндра на единицу его длины. Очевидно, что между двумя цилиндрами разность потенциала будет равна:
(3.1.61)
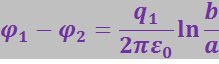
где b – радиус внешнего цилиндра, а точка 2 лежит на внутренней поверхности внешнего цилиндра.
Шаровой конденсатор. Имеются две концентрических сферы. Радиус внутренней сферы а, внешней – b. Напряжённость поля Е между такими сферами определяется формулой (3.1.41) и изменяется в пространстве так же, как и в случае точечного заряда. Следовательно, разность потенциалов между внутренней сферой и какой-либо точкой внутри конденсатора, удалённой на расстояние r от центра конденсатора, равна:
 ,
,
а разность потенциалов между двумя сферами будет равна:
(3.1.62)

В двух последних формулах q – заряд одной из сфер.
Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью. Её уравнение имеет вид
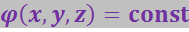
При перемещении по эквипотенциальной поверхности на отрезок ![]() потенциал не изменяется
потенциал не изменяется ![]() . Следовательно, согласно формуле (3.1.54) касательная к поверхности, составляющая вектора
. Следовательно, согласно формуле (3.1.54) касательная к поверхности, составляющая вектора ![]() , равна нулю. Отсюда следует, что вектор
, равна нулю. Отсюда следует, что вектор ![]() в каждой точке направлен по нормали к эквипотенциальной поверхности, проходящей через данную точку. Приняв во внимание, что вектор
в каждой точке направлен по нормали к эквипотенциальной поверхности, проходящей через данную точку. Приняв во внимание, что вектор ![]() направлен по касательной к линии
направлен по касательной к линии ![]() , легко сообразить, что линии напряжённости в каждой точке ортогональны к эквипотенциальным поверхностям.
, легко сообразить, что линии напряжённости в каждой точке ортогональны к эквипотенциальным поверхностям.
Эквипотенциальную поверхность можно провести через любую точку поля. Значит, таких поверхностей может быть построено бесконечное множество.
Условливаются проводить поверхности таким образом, чтобы разность потенциалов для двух соседних поверхностей была всюду одна и та же. Тогда по густоте эквипотенциальных поверхностей можно судить о величине напряжённости поля. Действительно, чем гуще располагаются эквипотенциальные поверхности, тем быстрее изменяется потенциал при перемещении вдоль нормали к поверхности. Следовательно, тем больше в данном месте ![]() , а значит и
, а значит и ![]() .
.
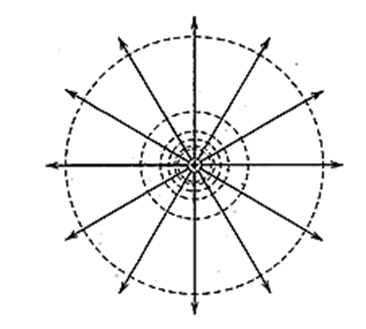
На рис. 3.1.28 показаны эквипотенциальные поверхности для поля точечного заряда. В соответствие с характером зависимости Е от r эквипотенциальные поверхности при приближении к заряду становятся гуще.
Для однородного поля эквипотенциальные поверхности представляют собой систему равноотстоящих друг от друга плоскостей, перпендикулярных к направлению поля.
Рис. 3.1.28 |
к к к