ФИЗИКА
3.1.9. Потенциал электрического поля
Пусть точечный заряд q', находящийся в поле неподвижного точечного заряда q, переместился вдоль изображённой на рис. 3.1.24 траектории из положения 1 в положение 2. Найдём работу A12, совершаемую при этом над зарядом q' силами поля, в котором он находится. На заряд q' действует кулоновская сила
(3.1.43)
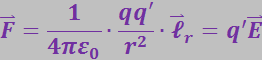
где Е – напряжённость поля, создаваемая зарядом q (направление силы на рис. 3.1.24 соответствует одноимённым зарядам q и q').
Рис. 3.1.24 |
Элементарная работа силы (3.1.43) равна:
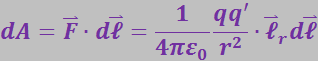
где ![]() – перемещение заряда q'.
– перемещение заряда q'.
На рис. 3.1.24 видно, что ![]() – приращению расстояния между q и q' (в точке А обе величины
– приращению расстояния между q и q' (в точке А обе величины ![]() и dr положительны, в точке В они отрицательны. С учётом этого для работы на пути 1-2 получается выражение:
и dr положительны, в точке В они отрицательны. С учётом этого для работы на пути 1-2 получается выражение:
(3.1.44)
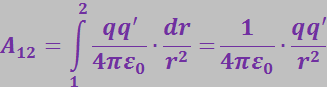
Полученный результат означает, что работа силы (3.1.43) не зависит от пути, по которому переместили заряд q', а лишь от начального и конечного положений заряда (от ![]() и
и ![]() ). Значит, кулоновская сила консервативна.
). Значит, кулоновская сила консервативна.
Из механики известно, что работа консервативных сил на любом замкнутом пути равна нулю. В случае электростатического поля эта работа определяется интегралом ![]() (кружок у знака интеграла означает, что интегрирование производится по замкнутому контуру). Приравняв этот интеграл нулю, придём к соотношению
(кружок у знака интеграла означает, что интегрирование производится по замкнутому контуру). Приравняв этот интеграл нулю, придём к соотношению
(3.1.45)
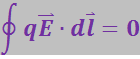 ,
,
которое должно выполнятся для любого замкнутого контура. Это соотношение называется циркуляцией вектора ![]() по данному контуру.
по данному контуру.
Таким образом, характерным для электростатического поля является то, что циркуляция вектора ![]() по любому замкнутому контуру равна нулю.
по любому замкнутому контуру равна нулю.
Надо иметь в виду, что условие (3.1.45) справедливо только для электростатического поля. Для поля движущихся зарядов это условие не выполняется.
Как известно, работа консервативных сил может быть представлена как убыль потенциальной энергии ![]() :
:
(3.1.46)
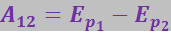
Сопоставление этого соотношения с (3.1.44) даёт для потенциальной энергии, которой обладает заряд q' в поле заряда q, выражение
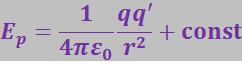
Значение константы обычно выбирается так, чтобы при удалении заряда q' от заряда q на бесконечность (т.е. при ![]() ) потенциальная энергия обращалась в нуль. При этом условии
) потенциальная энергия обращалась в нуль. При этом условии
(3.1.47)
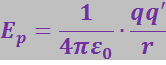
Воспользуемся зарядом q' в качестве пробного заряда для исследования поля. Согласно (3.1.47) потенциальная энергия, которой обладает пробный заряд, зависит не только от его величины q', но и от величин q и r, определяющих поле. Следовательно, эта энергия может быть использована для описания поля, подобно тому, как была использована для этой цели сила, действующая на пробный заряд.
Разные пробные заряды ![]() будут обладать в одной и той же точке поля различной энергией. Однако отношение
будут обладать в одной и той же точке поля различной энергией. Однако отношение ![]() будет для всех зарядов одним и тем же. Величина
будет для всех зарядов одним и тем же. Величина
(3.1.48)
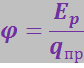
называется потенциалом поля в данной точке и используется, наряду с напряжённостью ![]() , для описания электрических полей.
, для описания электрических полей.
Из (3.1.48) следует, что потенциал численно равен потенциальной энергии, которой обладал бы в данной точке поля единичный положительный заряд. Подставив в (3.1.48) значение потенциальной энергии (3.1.47), получим для потенциала точечного заряда следующее выражение:
(3.1.49)
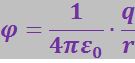
Рассмотрим поле, создаваемое системой N точечных зарядов ![]() . Расстояния от каждого из зарядов до данной точки поля обозначим
. Расстояния от каждого из зарядов до данной точки поля обозначим ![]() . Работа, совершаемая силами этого поля над зарядом q', будет равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности:
. Работа, совершаемая силами этого поля над зарядом q', будет равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности:
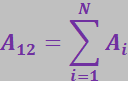
Каждая из работ ![]() согласно (3.1.44) равна:
согласно (3.1.44) равна:
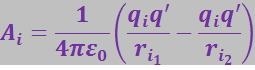
где ![]() – расстояние от заряда
– расстояние от заряда ![]() до начального положения заряда q';
до начального положения заряда q';
![]() – расстояние от
– расстояние от ![]() до конечного положения заряда q'.
до конечного положения заряда q'.
Следовательно,
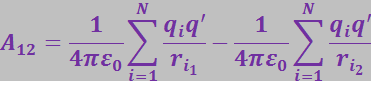
Сопоставив это выражение с соотношением (3.1.46), получим для потенциальной энергии заряда q' в поле системы зарядов выражение
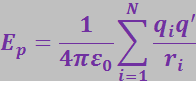 ,
,
из которого следует, что
(3.1.50)
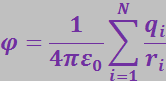
Сравнение полученной формулы с выражением (3.1.49) приводит к выводу, что потенциал поля, создаваемого системой зарядов равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности.
Из (3.1.48) следует, что заряд q, находящийся в точке поля с потенциалом φ, обладает потенциальной энергией
(3.1.51)
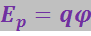
Отсюда, работа сил поля над зарядом q может быть выражена через разность потенциалов:
(3.1.52)
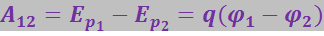
Если заряд q из точки с потенциалом φ удаляется на бесконечность (где по условию потенциал равен нулю) работа сил поля будет равна:
(3.1.53)

Отсюда следует, что потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки на бесконечность. Такую же по величине работу нужно совершить против сил поля для того, чтобы переместить единичный положительный заряд из бесконечности в данную точку поля.
В системе СИ за единицу потенциала, называемую вольтом (В), принимается потенциал в такой точке, для перемещения в которую из бесконечности заряда, равного 1 кулону, нужно совершить работу в 1 джоуль:
 ,
,
отсюда
 .
.
В физике часто пользуются единицей энергии и работы, называемой электрон-вольтом (эВ). Под электрон-вольтом подразумевается работа, совершаемая силами поля над зарядом, равным заряду электрона при прохождении им разности потенциалов в 1 В:
 .
.
Используя также кратные электрон-вольту единицы:
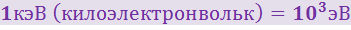
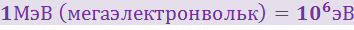
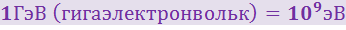
к к к