ФИЗИКА
3.1.8. Примеры вычисления напряжённости электростатических полей с помощью теоремы Гаусса
Поле бесконечной однородно заряженной плоскости. Когда заряд сосредоточен в тонком поверхностном слое тела, распределение заряда характеризуется с помощью поверхностной плотности σ, которая определяется выражением
(3.1.36)
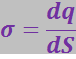
Под dS подразумевается физически бесконечно малый участок поверхности, dq – заряд, находящийся на этом участке.
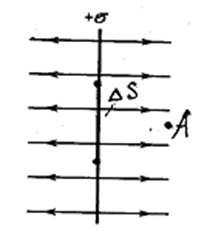
Пусть плоскость бесконечных размеров заряжена с одинаковой всюду поверхностной плотностью σ (рис. 3.1.15).
Рис. 3.1.15 |
Относительно любой точки (например, точки А на рис. 3.1.15) плоскость простирается во все стороны одинаково. Отсюда следует, что напряжённость может быть направлена только по нормали к плоскости. Поэтому линии поля представляют собой перпендикулярные к плоскости прямые линии, густота которых вследствие однородного распределения заряда всюду одна и та же. На участке ![]() поверхности сосредоточен заряд, равный
поверхности сосредоточен заряд, равный ![]() . Согласно формуле (3.1.31) на этом заряде начинаются
. Согласно формуле (3.1.31) на этом заряде начинаются ![]() линий, половина которых идёт в одну сторону от плоскости и половина – в другую. Следовательно, густота линий, а значит и напряжённость поля, равна
линий, половина которых идёт в одну сторону от плоскости и половина – в другую. Следовательно, густота линий, а значит и напряжённость поля, равна ![]() :
:
(3.1.37)
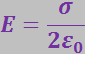
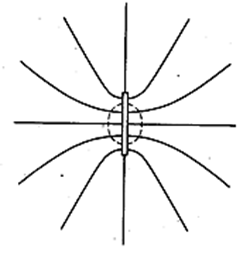
Если взять плоскость конечных размеров, например, заряженную тонкую пластинку (рис. 3.1.16), то полученный результат будет справедливым только для точек, расстояние которых от края пластинки значительно превышает расстояние от самой пластинки. По мере удаления от плоскости или приближения к её краям поле будет всё больше отличаться от поля бесконечной заряженной плоскости. Характер поля на больших расстояниях легко представить, если учесть, что на расстояниях значительно превышающих размеры пластинки, создаваемое ею поле можно рассматривать как поле точечного заряда.
Рис. 3.1.16 |
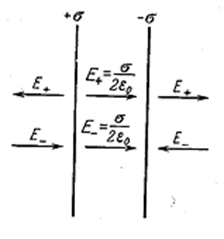
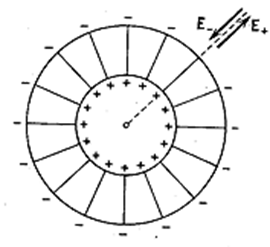
Поле двух разноименно заряженных бесконечных плоскостей. Пусть две параллельные бесконечные плоскости заряжены однородно с одинаковой поверхностной плотностью +σ и -σ (рис. 3.1.17).
Рис. 3.1.17 |
Каждая из плоскостей создаёт однородное поле с напряжённостью, определяемой формулой (3.1.37). На рис. 3.1.17 видно, что вне плоскостей результирующая напряжённость поля равна нулю. В пространстве между плоскостями поля имеют одинаковое направление, вследствие чего
(3.1.38)
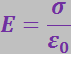
Таким образом, поле однородно и сосредоточено в зазоре между плоскостями. Полученный результат приближённо справедлив и для плоскостей конечных размеров, если расстояние между плоскостями много меньше их линейных размеров (плоский конденсатор). В этом случае заметные отклонения поля от однородности наблюдаются только вблизи краёв пластин.
Рис. 3.1.18 |
Поле однородно заряженного бесконечного цилиндра. Если заряд сосредоточен на очень тонком «нитевидном» проводнике, распределение заряда по нити характеризуют с помощью линейной плотности λ, определяемой выражением
(3.1.39)
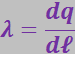
где ![]() – физически бесконечно малый отрезок нити;
– физически бесконечно малый отрезок нити;
![]() – заряд, находящийся на этом отрезке.
– заряд, находящийся на этом отрезке.
С помощью линейной плотности можно характеризовать и распределение заряда на цилиндрическом проводнике при условии, что в каждом сечении этого проводника заряд распределён однородно.
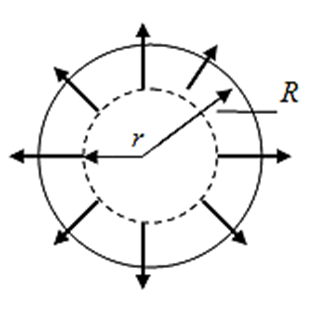
Найдём поле бесконечной цилиндрической поверхности радиуса R, заряженной однородно с линейной плотностью λ (рис. 3.1.19, на котором изображено поперечное сечение этого проводника).
Рис.3.1.19 |
Из соображений симметрии ясно, что линиями поля будут равномерно распределённые вокруг цилиндра радиальные прямые, начинающиеся (если ![]() ) либо оканчивающиеся (если
) либо оканчивающиеся (если ![]() ) на поверхности цилиндра. Внутри поверхности линии идти не могут, так как там нет зарядов, на которых они могли бы начинаться или оканчиваться. На отрезке длины
) на поверхности цилиндра. Внутри поверхности линии идти не могут, так как там нет зарядов, на которых они могли бы начинаться или оканчиваться. На отрезке длины ![]() находится заряд
находится заряд ![]() , на котором начинаются
, на котором начинаются ![]() линий поля. Их густота на расстоянии r от оси цилиндра равна
линий поля. Их густота на расстоянии r от оси цилиндра равна ![]() . Следовательно, внутри поверхности поле отсутствует, а вне цилиндра напряжённость поля определяется формулой
. Следовательно, внутри поверхности поле отсутствует, а вне цилиндра напряжённость поля определяется формулой
(3.1.40)
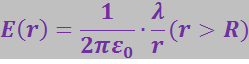
Из (3.1.40) следует, что, уменьшая радиус цилиндра, можно (при неизменной λ) получить вблизи поверхности цилиндра поле очень большой напряжённости.
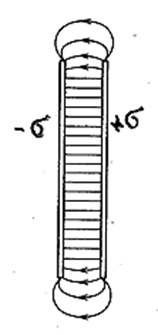
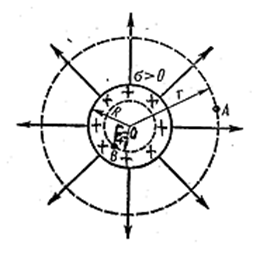
С помощью принципа суперпозиции легко найти поле двух коаксиальных цилиндрических поверхностей, заряженных с одинаковой по величине, но отличающейся знаком линейной плотностью λ (рис. 3.1.20).
Рис. 3.1.20 |
Внутри меньшего и вне большего цилиндров поле отсутствует. В зазоре между цилиндрами величина напряжённости поля определяется формулой (3.1.40). Это справедливо и для цилиндрических поверхностей конечной длины, если зазор между поверхностями много меньше их длины (цилиндрический конденсатор). Заметные отступления от поля поверхностей бесконечной длины будут наблюдаться только вблизи краёв цилиндров.
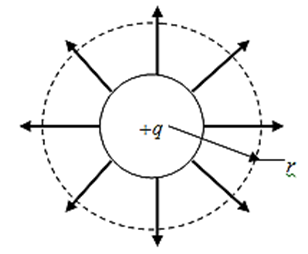
Поле однородно заряженной сферы. Предположим, что заряд q распределён однородно по сферической поверхности радиуса R (рис. 3.1.21).
Рис. 3.1.21 |
На этой поверхности начинаются ![]() линий. Их густота на расстоянии r от центра сферы равна
линий. Их густота на расстоянии r от центра сферы равна ![]() . Следовательно, напряжённость поля определяется выражением
. Следовательно, напряжённость поля определяется выражением
(3.1.41)
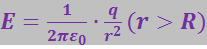
совпадающим с выражением для напряжённости поля точечного заряда q, помещённого в центре сферы.
В случае двух концентрических сферических поверхностей, по одной из которых распределён заряд +q, а по другой заряд -q, поле сосредоточено в зазоре между поверхностями. Напряжённость поля определяется формулой (3.1.41), где r – расстояние от общего центра сфер.
Поле объёмно заряженного шара. Допустим, что заряд q однородно распределён по объёму шара радиуса R (рис. 3.1.22). Внутренняя часть шара, ограниченная сферой радиуса r, содержит заряд, равный ![]() . В ней берут начало
. В ней берут начало ![]() линий поля. Густота этих линий на расстоянии r от центра равна
линий поля. Густота этих линий на расстоянии r от центра равна ![]() . Следовательно, напряжённость поля внутри шара определяется формулой
. Следовательно, напряжённость поля внутри шара определяется формулой
(3.1.42)
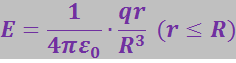
Рис. 3.1.22 |
Вне шара поле тождественно с полем, которое создавал бы точечный заряд q, помещённый в центр шара. На рис. 3.1.23 изображён график, показывающий изменение напряжённости поля с расстоянием от центра шара.
Рис. 3.1.23 |
к к к