ФИЗИКА
3.1.6. Поток и дивергенция векторного поля
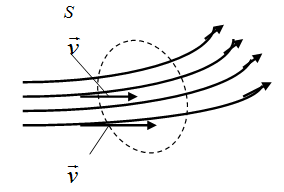
Нагляднее всего эти понятия оказываются в случае поля вектора скорости частиц текущей жидкости. Течение жидкости можно представить с помощью линий тока (рис. 3.1.8). Эти линии удовлетворяют двум условиям:
1) скорость частицы жидкости, проходящей через данную точку пространства, направлена по касательной к линии в данной точке;
2) густота линий численно равна модулю скорости частиц в данном месте потока.
Рис. 3.1.8 |
Рассмотрим стационарное (т.е. не изменяющееся со временем) течение несжимаемой жидкости. Поместим в поток воображаемую поверхность S (ограничивающий её контур изображён на рис. 3.1.8 штриховой линией). Потоком жидкости через поверхность S называется объём жидкости, проходящей через S в единицу времени.
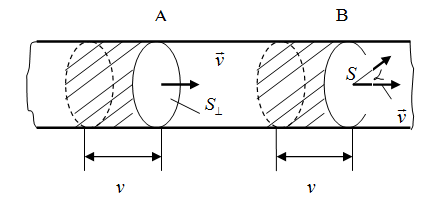
Проще всего вычислить поток в случае, когда жидкость течёт по цилиндрической трубе, причём скорость частиц жидкости во всех точках поперечного сечения трубы одинакова, т.е. поле вектора 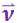 однородно (рис. 3.1.9). Очевидно, что в единицу времени через перпендикулярную к оси трубы поверхность
однородно (рис. 3.1.9). Очевидно, что в единицу времени через перпендикулярную к оси трубы поверхность ![]() пройдёт жидкость, заключённая в заштрихованном на рисунке цилиндре с основанием
пройдёт жидкость, заключённая в заштрихованном на рисунке цилиндре с основанием ![]() и высотой
и высотой 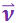 . Следовательно, обозначив поток жидкости
. Следовательно, обозначив поток жидкости ![]() можно написать
можно написать
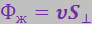
Рис. 3.1.9 |
Аналогично через плоскую поверхность S, образующую с поверхностью ![]() угол α, пройдёт в единицу времени жидкость, заключённая в косом цилиндре с основанием S и высотой
угол α, пройдёт в единицу времени жидкость, заключённая в косом цилиндре с основанием S и высотой ![]() . Объём этого цилиндра равен
. Объём этого цилиндра равен ![]() , где α– угол между вектором v и нормалью к поверхности
, где α– угол между вектором v и нормалью к поверхности 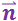 . Таким образом, поток через S равен:
. Таким образом, поток через S равен:
(3.1.19)

где ![]() – проекция v на нормаль
– проекция v на нормаль 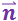 .
.
Нормаль 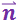 можно направить как в одну, так и в другую сторону от плоскости, причём оба направления совершенно равноправны. В случае, изображённом на рис. 3.1.9, нормаль образует с
можно направить как в одну, так и в другую сторону от плоскости, причём оба направления совершенно равноправны. В случае, изображённом на рис. 3.1.9, нормаль образует с 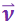 острый угол, вследствие чего
острый угол, вследствие чего ![]() , а следовательно, и
, а следовательно, и ![]() оказываются положительными. Однако, если бы мы направили нормаль в противоположную сторону,
оказываются положительными. Однако, если бы мы направили нормаль в противоположную сторону, ![]() , а следовательно, и
, а следовательно, и ![]() были бы отрицательными. Таким образом, поток (3.1.19) является величиной алгебраической; его знак зависит от выбора направления нормали к поверхности, через которую вычисляется поток.
были бы отрицательными. Таким образом, поток (3.1.19) является величиной алгебраической; его знак зависит от выбора направления нормали к поверхности, через которую вычисляется поток.
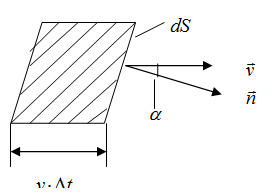
Чтобы вычислить поток в случае, изображённом на рис. 3.1.8, нужно разбить поверхность на элементарные участки dS. Поток ![]() через такой участок можно вычислить по формуле 3.1.19:
через такой участок можно вычислить по формуле 3.1.19:
(3.1.20)

где v – модуль скорости в том месте, где расположена площадка dS (рис. 3.1.10)
Рис. 3.1.10 |
Введём вектор ![]() , модуль которого равен dS, а направление совпадает с направлением нормали
, модуль которого равен dS, а направление совпадает с направлением нормали 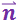 к площадке
к площадке ![]() . Поскольку направление нормали выбирается условно,
. Поскольку направление нормали выбирается условно, 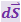 является псевдовектором. Угол α между векторами
является псевдовектором. Угол α между векторами 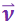 и
и 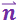 (рис. 3.1.10) является также углом между векторами
(рис. 3.1.10) является также углом между векторами 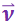 и
и ![]() . Поэтому формулу (3.1.20) можно написать в виде скалярного произведения векторов
. Поэтому формулу (3.1.20) можно написать в виде скалярного произведения векторов 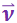 и
и ![]() :
:
(3.1.21)
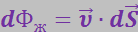
Просуммировав выражение (3.1.21) по всей поверхности S, получим поток жидкости через эту поверхность:
(3.1.22)
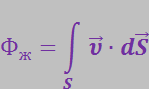
Выражение (3.1.22) получено для поля вектора скорости частиц жидкости. Аналогичное выражение, написанное для вектора напряжённости электрического поля ![]() называется потоком вектора
называется потоком вектора ![]() через поверхность S:
через поверхность S:
(3.1.23)
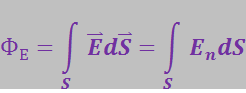
где ![]() – поток вектора
– поток вектора ![]() .
.
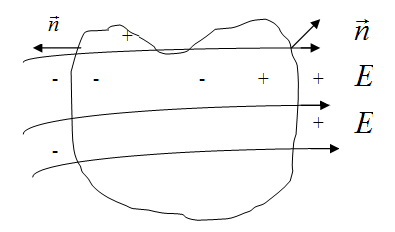
В электростатике обычно считаются потоки входящие или выходящие из данной поверхности.
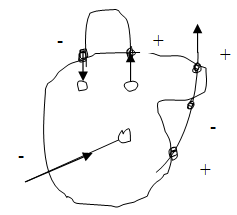
В этом случае условились считать за положительное направление нормали направление наружу. Поэтому пересечения при выходе линий напряжённости наружу будут положительными, а пересечения при входе линий внутрь – отрицательными (рис. 3.1.11). В соответствии с этим, поток, выходящий из ограниченного поверхностью объёма наружу, оказывается положительным, а поток, входящий внутрь – отрицательным.
Рис. 3.1.11 |
На рис. 3.1.11 видно, что в случае, когда линии поля проходят внутри замкнутой поверхности не прерываясь, каждая линия пересекая поверхность, входит внутрь и выходит наружу одинаковое число раз. В итоге полное число положительных пересечений будет равно полному числу отрицательных пересечений и поток вектора через поверхность оказывается равным нулю.
Из рис. 3.1.12 следует, что линия, начинающаяся внутри замкнутой поверхности, вносит в поток вклад, равный +1, а линия, оканчивающаяся внутри поверхности – вклад, равный -1. Отсюда заключаем, что поток вектора ![]() через замкнутую поверхность численно равен разности линий, начинающихся внутри поверхности
через замкнутую поверхность численно равен разности линий, начинающихся внутри поверхности ![]() , и числа линий, оканчивающихся внутри поверхности
, и числа линий, оканчивающихся внутри поверхности ![]() :
:
(3.1.24)

Размерности слева и справа не совпадают. Поэтому знак равенства взят в скобки. Отметим, что линии, начинающиеся и оканчивающиеся внутри замкнутой поверхности, вклада в поток не вносят.
Рис. 3.1.12 |
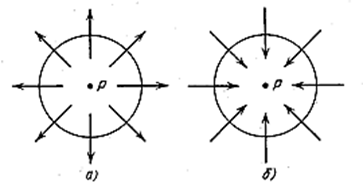
Рассмотрим точку Р, в окрестности которой начинаются (рис. 3.1.13а) либо оканчиваются (рис. 3.1.13б) линии поля. Назовём дивергенцией (от лат. divergentia – расхождение) векторного поля ![]() в точке Р величину, численно равную плотности точек (т.е. количеству точек, приходящихся на единицу объёма), в которых начинаются либо оканчиваются линии поля.
в точке Р величину, численно равную плотности точек (т.е. количеству точек, приходящихся на единицу объёма), в которых начинаются либо оканчиваются линии поля.
Рис. 3.1.13 |
В первом случае будем считать дивергенцию положительной, во втором – отрицательной (схождение линий равнозначно отрицательному расхождению).
Выделим в окрестности точки Р объём V очень малых линейных размеров. Если внутрь этого объёма попадёт ![]() точек, в которых начинаются линии поля, либо -
точек, в которых начинаются линии поля, либо - ![]() точек, в которых оканчиваются линии поля, то дивергенция будет равна:
точек, в которых оканчиваются линии поля, то дивергенция будет равна:
(3.1.25)
 ;
;

Согласно формуле (3.1.24) ![]() в первом случае и -
в первом случае и - ![]() во втором случае численно равны потоку вектора
во втором случае численно равны потоку вектора ![]() через ограничивающую объём V поверхность S. Поэтому оба соотношения (3.1.25) можно представить одной формулой
через ограничивающую объём V поверхность S. Поэтому оба соотношения (3.1.25) можно представить одной формулой
(3.1.26)
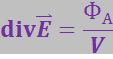
(в этой формуле левая и правая части имею одинаковую размерность, поэтому знак равенства не взят в скобки).
Если точки, в которых начинаются или оканчиваются линии поля, распределены в пространстве неравномерно, то для получения значения дивергенции в точке Р нужно взять предел выражения (3.1.26) при условии, что V стремится к нулю, стягиваясь к точке Р. Заметив в дополнение к этому ![]() согласно (3.1.23), придём к строгому математическому определению дивергенции:
согласно (3.1.23), придём к строгому математическому определению дивергенции:
(3.1.27)
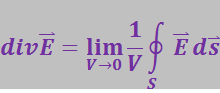
(S – поверхность, ограничивающая объём V).
Дивергенция – скалярная величина, которая может быть как положительной, так и отрицательной. Существует два способа обозначения дивергенции: ![]() и
и ![]() , где
, где ![]() (набла) – векторный дифференциальный оператор:
(набла) – векторный дифференциальный оператор:
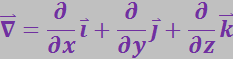
Точки, в которых начинаются линии поля, естественно назвать источниками поля. Тогда дивергенцию можно трактовать как мощность источников поля, отнесённую к единице объёма. Точки, в которых оканчиваются линии поля, называются стоками.
Согласно формуле (3.1.25) выражение ![]() даёт
даёт ![]() , т.е. число линий поля, начинающихся в объёме
, т.е. число линий поля, начинающихся в объёме ![]() , либо -
, либо - ![]() , т.е. взятое со знаком минус число линий поля, оканчивающихся в объёме
, т.е. взятое со знаком минус число линий поля, оканчивающихся в объёме ![]() .
.
Следовательно,
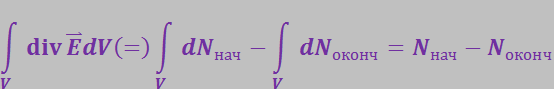 ,
,
где все три интеграла берутся по одному и тому же конечному объёму V.
Из (3.1.25) следует, что правая часть полученного нами соотношения представляет собой поток вектора ![]() через замкнутую поверхность S, ограничивающую объём V. Таким образом,
через замкнутую поверхность S, ограничивающую объём V. Таким образом,
(3.1.28)
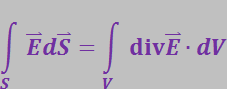
Это соотношение называют теоремой Остроградского-Гаусса.
к к к