ФИЗИКА
3.1.5. Поле электрического диполя
Основная задача электростатики заключается в том, чтобы по заданным распределению в пространстве и величине источников поля – электрических зарядов – найти величину и направление вектора напряжённости ![]() в каждой точке поля.
в каждой точке поля.
Приведём пример решения этой задачи с помощью принципа суперпозиции полей. Рассмотрим поле электрического диполя.
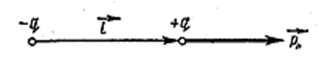
Электрическим диполем называют систему двух равных по величине и противоположных по знаку электрических зарядов +q и -q, расстояние между которыми мало по сравнению с расстоянием до рассматриваемых точек поля. Оказалось, что молекулы диэлектриков по своим электрическим свойствам подобны диполям. Поэтому изучение поля диполя представляет собой большой практический интерес.
Введём некоторые определения. Плечом диполя называется вектор ![]() , направленный по оси диполя от отрицательного заряда к положительному и численно равный расстоянию между ними (рис. 3.1.4). Произведение положительного заряда диполя q на плечо
, направленный по оси диполя от отрицательного заряда к положительному и численно равный расстоянию между ними (рис. 3.1.4). Произведение положительного заряда диполя q на плечо 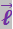 называется электрическим моментом диполя
называется электрическим моментом диполя ![]()
(3.1.9)
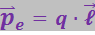
Рис. 3.1.4 |
Вектор ![]() совпадает по направлению с плечом диполя
совпадает по направлению с плечом диполя ![]() .
.
В соответствии с принципом суперпозиции полей напряжённость ![]() в произвольной точке поля диполя равна
в произвольной точке поля диполя равна
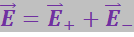 ,
,
где E+ и E- – напряжённости полей зарядов +q и -q.
Рис. 3.1.5 |
Если точка А расположена на оси диполя (рис. 3.1.5), то векторы ![]() и
и ![]() направлены также вдоль этой оси, но в противоположные стороны. По формуле (3.1.6)
направлены также вдоль этой оси, но в противоположные стороны. По формуле (3.1.6)
(3.1.10)
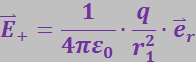
(3.1.11)
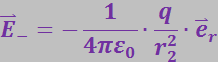
где ![]() и
и ![]() – расстояния соответственно от положительного и отрицательного зарядов до точки А.
– расстояния соответственно от положительного и отрицательного зарядов до точки А.
Подставив эти расстояния в (3.1.10) и (3.1.11), получим
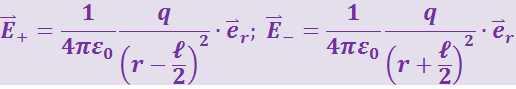
и
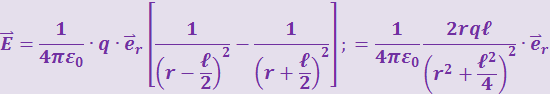
Заменяя в последнем равенстве ![]() , будем иметь
, будем иметь
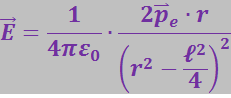
Если расстояние r во много раз больше длины диполя ![]() , то членом
, то членом ![]() по сравнению с r2 можно пренебречь. Тогда
по сравнению с r2 можно пренебречь. Тогда
(3.1.12)
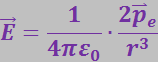
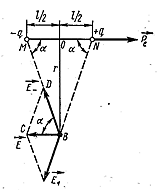
Найдём выражение для напряжённости поля диполя в точке В, расположенной на перпендикуляре, восстановленном к оси диполя из его середины О (рис. 3.1.6).
Рис. 3.1.6 |
Точка В равноудалена от зарядов +q и -q. Поэтому
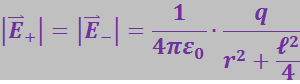
Треугольники BMN и BCD – равнобедренные, причём углы при вершинах М и N ΔBMN и при вершинах В и С ΔBCD одинаковы и равны α. Так как стороны ВМ и BD, а также BN и DC попарно параллельны, т.е. вектор ![]() антипараллелен электрическому моменту диполя
антипараллелен электрическому моменту диполя ![]()
(3.1.13)
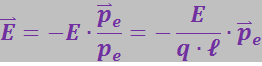
Из рис. 3.1.6 видно, что численное значение Е напряжённости поля в точке В равно:

или
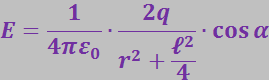
Из ΔBMD:
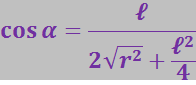
Поэтому
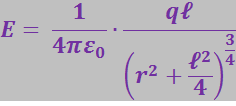
Пренебрегая величиной ![]() по сравнению с r2, получим:
по сравнению с r2, получим:
(3.1.14)
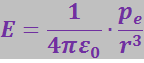
Из (3.1.13) и (3.1.14) следует, что вектор напряжённости поля в точке В равен:
(3.1.15)
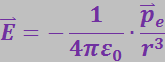
Рассмотрим далее самый общий случай. Пусть точка С лежит на расстоянии r от середины О диполя, причём радиус-вектор  образует с осью диполя угол φ (рис. 3.1.7).
образует с осью диполя угол φ (рис. 3.1.7).
Рис. 3.1.7 |
Соединим пунктиром заряды -q и +q с точкой С и опустим на прямую NC перпендикуляр из точки М. Поместим в основании К этого перпендикуляра два точечных заряда +q и -q. Расположенные в одной и той же точке равные по величине и противоположные по знаку заряды +q и -q полностью нейтрализуют друг друга и не искажают поля диполя. Четыре заряда, находящиеся в точках М, N, и К, можно рассматривать как два диполя (NK и МК). Ввиду малости расстояния ![]() по сравнению с r угол CNM = φ. Поэтому электрические моменты первого и второго диполей соответственно равны:
по сравнению с r угол CNM = φ. Поэтому электрические моменты первого и второго диполей соответственно равны:
(3.1.16)


Для первого диполя точка С лежит на его оси, а для второго – на перпендикуляре, восстановленном в средней точке оси. По формулам (3.1.12) и (3.1.13) напряжённости ![]() и
и ![]() , полей, создаваемых в точке С каждым из диполей, равны:
, полей, создаваемых в точке С каждым из диполей, равны:
 и
и 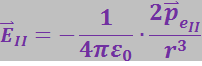
Векторы ![]() и
и ![]() взаимно перпендикулярны. Следовательно, векторы
взаимно перпендикулярны. Следовательно, векторы ![]() и
и ![]() тоже взаимно перпендикулярны. Поэтому численное значение Е напряжённости поля диполя MN в точке С равно:
тоже взаимно перпендикулярны. Поэтому численное значение Е напряжённости поля диполя MN в точке С равно:
(3.1.17)
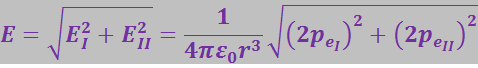
Подставив в (3.1.17) значения ![]() и
и ![]() из (3.1.16), получим:
из (3.1.16), получим:
(3.1.18)
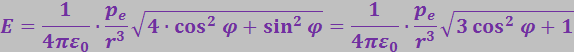
Формула (3.1.18) охватывает все возможные случаи расположения точки С. При φ = 0 она совпадает с (3.1.12), а при φ =π/2 - с (3.1.14).
Из формулы (3.1.18) следует, что напряжённость электрического поля диполя зависит от направления радиуса-вектора ![]() относительно оси диполя и убывает пропорционально кубу расстояния r от его центра, т.е. значительно быстрее, чем в случае одного точечного заряда. В связи с этим сила взаимодействия двух диполей оказывается обратно пропорциональной четвёртой степени расстояния между ними. Ещё быстрее убывает с расстоянием напряжённость поля квадруполя – системы двух одинаковых антипараллельных диполей, заряды которых расположены в вершинах небольшого квадрата. Для квадруполя Е пропорциональна r -4, а сила взаимодействия двух квадруполей F пропорциональна r -6. Чем больше число пар разноимённых зарядов и чем симметричнее они расположены в теле, тем быстрее убывает напряжённость поля в зависимости от расстояния.
относительно оси диполя и убывает пропорционально кубу расстояния r от его центра, т.е. значительно быстрее, чем в случае одного точечного заряда. В связи с этим сила взаимодействия двух диполей оказывается обратно пропорциональной четвёртой степени расстояния между ними. Ещё быстрее убывает с расстоянием напряжённость поля квадруполя – системы двух одинаковых антипараллельных диполей, заряды которых расположены в вершинах небольшого квадрата. Для квадруполя Е пропорциональна r -4, а сила взаимодействия двух квадруполей F пропорциональна r -6. Чем больше число пар разноимённых зарядов и чем симметричнее они расположены в теле, тем быстрее убывает напряжённость поля в зависимости от расстояния.
к к к