ФИЗИКА
3.1.3. Электрическое поле. Напряжённость поля
Взаимодействие между покоящимися зарядами осуществляется через электрическое поле. Всякий заряд изменяет свойства окружающего его пространства – создаёт в нём электрическое поле. Это поле проявляет себя тем, что на помещённый в какую-либо его точку электрический заряд действует сила, по величине которой можно судить об «интенсивности» поля.
Итак, для обнаружения и исследования электрического поля нужно воспользоваться некоторым «пробным» зарядом. Для того чтобы сила, действующая на пробный заряд, характеризовала поле «в данной точке», пробный заряд должен быть точечным и настолько малым, чтобы его внесение в исследуемое поле не изменяло поле. По знаку пробный заряд выбирают положительным.
Исследуем с помощью точечного пробного заряда qпр поле, создаваемое неподвижным положительным точечным зарядом q. Поместив пробный заряд в точку, положение которой относительно заряда q определяется радиус-вектором 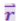 (рис. 3.1.1), мы обнаружим, что на пробный заряд согласно (3.1.2) действует сила
(рис. 3.1.1), мы обнаружим, что на пробный заряд согласно (3.1.2) действует сила
(3.1.4)
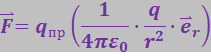
где ![]() - орт радиус-вектора
- орт радиус-вектора 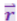 .
.
Рис. 3.1.1 |
Из (3.1.4) следует, что сила, действующая на пробный заряд, зависит не только от величин, определяющих поле (от q и  ), но и от величины пробного заряда qпр. Если брать разные по величине точечные заряды, то и силы, которые они испытывают в данной точке поля, будут различными. Однако отношение
), но и от величины пробного заряда qпр. Если брать разные по величине точечные заряды, то и силы, которые они испытывают в данной точке поля, будут различными. Однако отношение ![]() для всех пробных зарядов будет одним и тем же и, как видно из (3.1.4), оно зависит лишь от величин q и r, определяющих поле в данной точке. Поэтому естественно принять это отношение в качестве величины, характеризующей электрическое поле:
для всех пробных зарядов будет одним и тем же и, как видно из (3.1.4), оно зависит лишь от величин q и r, определяющих поле в данной точке. Поэтому естественно принять это отношение в качестве величины, характеризующей электрическое поле:
(3.1.5)
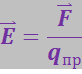
Эту векторную величину называют напряжённостью электрического поля в данной точке.
В соответствии с формулой (3.1.5) напряжённость электрического поля численно равна силе, действующей на единичный точечный заряд, находящийся в данной точке поля. Направление вектора ![]() совпадает с направлением силы, действующей на положительный заряд.
совпадает с направлением силы, действующей на положительный заряд.
Из (3.1.4) и (3.1.5) следует, что напряжённость поля точечного заряда пропорциональна величине заряда q и обратно пропорциональна квадрату расстояния r от заряда до данной точки поля
(3.1.6)
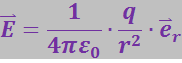
Направлен вектор ![]() вдоль радиальной прямой, проходящей через заряд в данную точку поля, от заряда, если он положителен, и к заряду, если он отрицателен.
вдоль радиальной прямой, проходящей через заряд в данную точку поля, от заряда, если он положителен, и к заряду, если он отрицателен.
За единицу напряжённости поля принимается напряжённость в такой точке, в которой на заряд, равный 1Кл действует сила 1 Н. В СИ единица напряжённости электрического поля имеет название вольт на метр и обозначается В/м.
Из (3.1.5) следует: на всякий точечный заряд q в точке с напряжённостью ![]() будет действовать сила
будет действовать сила
(3.1.7)
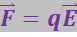
Эксперименты показывают, что сила, с которой система зарядов действует на некоторый не входящий в систему заряд, равна векторной сумме сил, с которыми действует на данный заряд каждый из зарядов в отдельности. Отсюда вытекает, что напряжённость поля системы зарядов равна векторной сумме напряжённостей полей, которые создавал бы каждый из зарядов системы в отдельности:
(3.1.8)
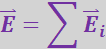
Последнее утверждение носит название принципа суперпозиции электрических полей.
Принцип суперпозиции позволяет вычислить напряжённость поля любой системы зарядов. Разбив протяжённые заряды на достаточно малые доли dq, любую систему зарядов можно свести к совокупности точечных зарядов. Вклад каждого из таких зарядов в результирующее поле вычисляется по (3.1.6).
Установлено, что принцип суперпозиции соблюдается вплоть до очень больших напряжённостей полей. Его правильность для напряжённостей полей в несколько миллионов вольт на метр (ускорители, высоковольтные разряды и т.д.) хорошо подтверждается всей инженерной практикой. Более значительные напряжённости поля имеются в атомах и ядрах. На орбитах электронов в атомах они равны ![]() . Рассчитанные в соответствии с принципом суперпозиции разности энергетических уровней атомов подтверждены экспериментально с большой степенью точности. Это означает, что и принцип суперпозиции при напряжённости внутриатомных полей соблюдается с большой точностью. На поверхности тяжёлых ядер напряжённости достигают громадных значений
. Рассчитанные в соответствии с принципом суперпозиции разности энергетических уровней атомов подтверждены экспериментально с большой степенью точности. Это означает, что и принцип суперпозиции при напряжённости внутриатомных полей соблюдается с большой точностью. На поверхности тяжёлых ядер напряжённости достигают громадных значений ![]() . Экспериментальные данные свидетельствуют, что и для этих громадных напряжённостей принцип суперпозиции выполняется.
. Экспериментальные данные свидетельствуют, что и для этих громадных напряжённостей принцип суперпозиции выполняется.
к к к